(see gflownet tutorial and paper list here)
I have rarely been as enthusiastic about a new research direction. We call them GFlowNets, for Generative Flow Networks. They live somewhere at the intersection of reinforcement learning, deep generative models and energy-based probabilistic modelling. They are also related to variational models and inference and I believe open new doors for non-parametric Bayesian modelling, generative active learning, and unsupervised or self-supervised learning of abstract representations to disentangle both the explanatory causal factors and the mechanisms that relate them. What I find exciting is that they open so many doors, but in particular for implementing the system 2 inductive biases I have been discussing in many of my papers and talks since 2017, that I argue are important to incorporate causality and deal with out-of-distribution generalization in a rational way. They allow neural nets to model distributions over data structures like graphs (for example molecules, as in the NeurIPS paper, or explanatory and causal graphs, in current and upcoming work), to sample from them as well as to estimate all kinds of probabilistic quantities (like free energies, conditional probabilities on arbitrary subsets of variables, or partition functions) which otherwise look intractable.
At the same time, this is a new beast which may, at first, look strange, one that we need to tame, for which the appropriate optimization algorithms are still making rapid progress (e.g. see this paper), and many opportunities probably waiting for us in upcoming research. It has taken time for many of my students to digest the new concepts, but it is worth it. A volley of new papers are coming out and more are in preparation, as the creative juices are boiling. My son Emmanuel led the first paper on GFlowNets and wrote a blog entry about it to accompany our NeurIPS 2021 paper, the original GFlowNet paper. More recently, I have written a tutorial to explain the basic ideas, and you will also find there all the recent publicly available papers. See also this rather technical talk I recently gave internally at Mila and this more accessible and philosophical discussion about GFlowNets, causality and consciousness providing a window on upcoming developments of GFlowNets aimed at bridging the gap between SOTA AI and human intelligence by introducing system 2 inductive biases in neural nets. Enjoy!
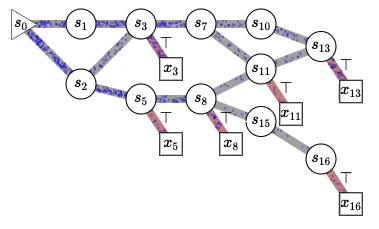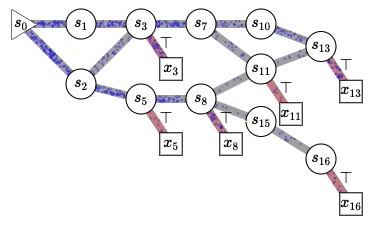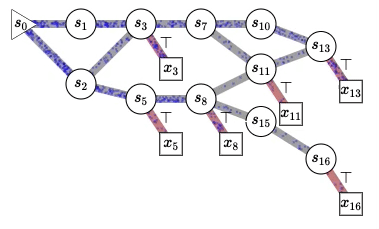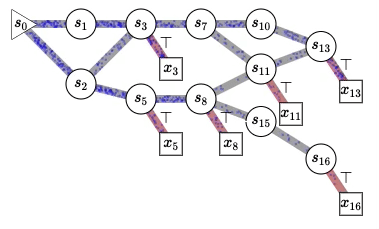
This figure illustrates why we use the word “flow” in GFlowNets. We think about the flow of unnormalized probabilities, similar to the amount of water flowing from an initial state (s0 on the left) in a directed acyclic graph (that may be exponentially large, so we don’t need to represent it explicitly in computers) whose trajectories correspond to all the possible sequences of actions, actions that determine state transitions) in order to sequentially construct complicated objects like molecular graphs, causal graphs, explanations for a scene, or (and this is the real inspiration) thoughts in our mind. The square nodes with red transitions correspond to terminal states, completed objects sampled by a policy which chooses stochastically the children of each state (the states accessible by going one step downstream) with a probability proportional to the flow in the corresponding outgoing edge. Interestingly, this makes it possible to generate a diverse set of samples without facing what I used to think was the intractable challenge of mixing between modes with MCMC methods. What is remarkable with this framework is that it tells us how to train a policy that will sample the constructed objects with the desired probability (specified by an energy function or unnormalized probability function or reward function, which we can also learn) and how to estimate the corresponding normalizing constants and conditional probabilities over any subset of abstract variables. See more in the tutorial 🙂