Intuitive understanding of MFCCs. The mel frequency cepstral coefficients… | by Emmanuel Deruty | Medium
Excerpt
The mel frequency cepstral coefficients (MFCCs) of an audio signal are a small set of features (usually about 10–20) which describe the overall shape of the spectral envelope. MFCCs were frequently…
[

](https://medium.com/@derutycsl?source=post_page-----836d36a1f779--------------------------------)
The mel frequency cepstral coefficients (MFCCs) of an audio signal are a small set of features (usually about 10–20) which describe the overall shape of the spectral envelope. MFCCs were frequently used for voice recognition (see for instance [Muda et al., 2010]) before the task started to be performed using deep learning (see for instance [Yu and Deng, 2016]). It was also used to describe “timbre”.
In particular, [Mauch et. al, 2015] use MFCCs as a descriptor for “timbre” in a study that describes the evolution of popular music. For a more detailed description of the process they use, see the Appendix.
One of their conclusions is that “[t]he decline in topic diversity and disparity [in popular music] in the early 1980s is due to a decline of timbral […] diversity”.
The underlying hypothesis to the conclusion is that MFCCs describe “timbre”. “Timbre” is not a well-defined notion. It has been described as highly multi-dimensional [Peeters et al., 2011]. It is therefore interesting, to better understand if MFCCs can describe “timbre” and to be able to interpret [Mauch et. al, 2015]’s conclusion, to provide an intuitive interpretation of MFCCs.
MFCCs part 1: DCT of a log(FFT)
The Aalto University wiki provides a clear overview of MFCCs. The extraction of MFCCs from an audio input is summarised in Figure 1. A log power spectrum is evaluated from the audio input. The power spectrum is resampled on the mel scale. The MFCC output is the Discrete Cosine Transform of the resampled spectrum. A significant dimensionality reduction comes from the resampling to the 16-band mel filter bank.
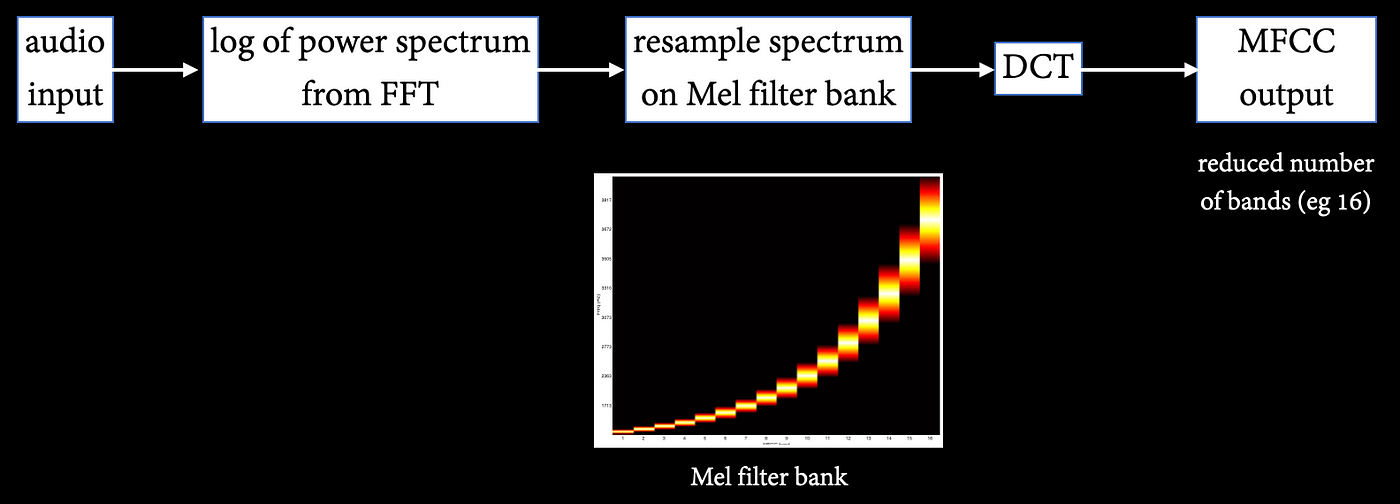
Figure 1. MFCC: principle.
As illustrated on Figure 2, the evaluation of the MFCCs involves two changes of domain: from time domain to frequency domain (FT) and then back to time domain (DCT). MFCCs are expressed in the time domain, the unit for MFCC coefficients is a unit of time.

Figure 2. Domains.
The successive FT and DCT make the MFCCs a “spectrum of a spectrum”. What does it mean? As illustrated on Figure 3, let’s try to intuitively interpret what may be the DCT of a log(FT) — first removing the mel-scale filtering.

Figure 3. “Spectrum of spectrum” — what does it mean?
To interpret the DCT of a log(abs(FT)), let’s start with a sine wave. The top image in Figure 4 shows the waveform for the 1000Hz sine wave. The image immediately below shows the log(FT) of the sine wave: a single frequency peak. The bottom (non-greyed) image is the DCT of the log (FT).
As mentioned above, a spectrum of a spectrum is in the time domain. The X-scale in the DCT of log(abs(FT)) is therefore a time scale (short durations / high frequencies on the left, long durations / low frequencies on the right). We choose to use frequency units to describe this time scale, so as to always express X-scales in Hz.

Figure 4. Input sine wave (time domain), log(FT) (frequency domain) and DCT of log(abs(FT)) (back to time domain).
In Figure 5, we compare the DCT of log(abs(FT)) to the autocorrelation of the input signal — more specifically, to the absolute value of the normalised autocorrelation.
Why introduce autocorrelation? Contrarily to DCT of log(abs(FT)), autocorrelation is a notion that can be intuitively understood. Autocorrelation quantifies the self-similarity of the signal at different time scales. If autocorrelation is at least partially similar to DCT of log(abs(FT)) (which happens to be the case), then we become able to provide an intuitive interpretation of the DCT of log(abs(FT)).

Figure 5. DCT of FT is related to autocorrelation.
Looking at Figure 5, it is obvious that autocorrelation is correlated to the DCT of log(abs(FT)), particularly at high frequencies. The observation is confirmed by the representations in Figure 6. The left diagram includes autocorrelation and DCT of log(abs(FT)) values for all frequencies. The right diagram shows these values for higher frequencies only. There is a high correlation between autocorrelation and DCT of log(abs(FT)) for high frequencies.

Figure 6. Especially at high frequencies.
In Figure 7, bottom, we zoom in on the high frequencies for both representations. Autocorrelation and DCT of log(abs(FT)) are nearly identical.

Figure 7. Abs (autocorrelation) and DCT of log(FT) are almost identical at high frequencies.
We can conclude that DCT of log(abs(FT)) can be interpreted as abs(normalised autocorrelation) for frequencies above ca. 800Hz.
An interesting question at this point is: as they are so similar, is there any advantage to using DCT of log(abs(FT)) over autocorrelation? Autocorrelation seems to be a much simpler process than DCT of log(abs(FT)).
Figure 8 illustrates what may be part of the answer. DCT of log(abs(FT)) is robust to the removal of the fundamental frequency, whereas autocorrelation isn’t. MFCCs were used in voice recognition tasks. Recognition should be possible when the speaker is on the phone for instance — a case in which it is likely that the fundamental will be missing due to bandpass filtering.

Figure 8. Why DCT(FT) instead of autocorrelation?
Perhaps because DCT(FT) is robust to missing fundamentals, and autocorrelation is not.
MFCCs part 2: Mel scale resampling of the FT
As seen above, MFCCs are not simply the DCT of log(abs(FT)), they are the DCT of the mel scale resampling of the log(abs(FT)). Let’s try to understand the influence of such resampling on MFCC evaluation.
The mel scale resampling is downsampling, it causes dimensional reduction. From the high number of initial log(abs(FT)) values (half the number of values of the original signal), the downsampling results in 16 values.
The downsampling process can also be interpreted as a low-pass filter of the log(abs(FT)). The rightmost image in Figure 9 shows the downsampled / low-pass filtered log(abs(FT)).

Figure 9. Mel filtering is low-pass filtering of the spectrum.
As illustrated in Figure 10, top, one consequence of the downsampling is the blurring of the pitch — indeed, pitch is irrelevant to both voice recognition and timbre description.
Perhaps more fundamentally — low-pass filtering a spectrum, what does it mean? Low-pass filtering of a signal (time domain) attenuates the high frequencies. Therefore, low-pass filtering of a spectrum (frequency domain) attenuates the high periods — which means attenuating the low frequencies. Low-pass filtering of a spectrum is high-pass filtering of the original signal.
Furthermore, as illustrated in Figure 10, bottom, mel-scale downsampling uses increasingly wide bands (in linear scale). This particular setting of bands gives comparatively more importance to the higher frequencies. From Figure 10, top, content above band 4 (670–1000Hz) appears to be emphasised in comparison to the content below. Notice how these frequencies correspond to the frequencies above which the DCT of log(abs(FT)) can be interpreted as abs(normalised autocorrelation).

Figure 10. Two consequences of the low pass filtering of the spectrum.
Since mel-scale downsampling is a filter, we can listen to how this filter sounds like. What should we listen to? During MFCC evaluation, the filter is applied to log(abs(FT)) — the power spectrum. The phase information is absent from the power spectrum. Therefore, the output of the filter should be listened to on audio from which the phase was removed. To conserve intelligibility in the original audio, we produce such a file by modulating white noise with the windowed power spectrum (=random phase). Mel-based filtering will be applied to this file.
Video 1 includes three audio extracts. The first extract is the initial audio, a spoken voice. The second extract is the corresponding “phaseless” audio. The third extract is the filtered “phaseless” audio.
The MFCCs can be interpreted as the DCT of the power spectrum of the third extract.
Video 1. Illustration of mel-scale filtering. 1) Original audio. 2) Power spectrum of original audio on white noise (for comparison with 3). 3) Mel-filtered spectrum on white noise.
MFCCs part 3: Autocorrelation and MFCCs
In part 1, we established that the DCT of log(abs(FT)) can be interpreted as abs(normalised autocorrelation) for frequencies above 800Hz. In part 2, we explicited the role of mel-scale resampling (high-pass filter + emphasis on high frequencies). Is it now possible to find a relation between the DCT of the resampled log(abs(FT)) — i.e. the MFCCs, and autocorrelation?
Figure 11, bottom right, shows the MFCCs for the original 1000Hz sine wave input. As such, they can’t be compared to autocorrelation, as the X-axis is not expressed on the same scale as autocorrelation.

Figure 11. DCT of fitered FFT.
Let’s evaluate the windowed MFCCs for the speech audio extract featured in part 2, along with the DCT of log(abs(FT)) and abs(normalised autocorrelation). The result is shown in Figure 12.

Figure 12. Find the relation between MFCC and correlation: a windowed example (speech).
A comparison between abs(normalised autocorrelation) at higher frequencies and the MFCCs shows similarities. At the very least, periodic/harmonic parts of the signal provide similar patterns. This observation can be verified by checking the correlation between abs(normalised autocorrelation) at higher frequencies and the MFCCs, the result of which is shown on the right.
The higher frequencies of abs(normalised autocorrelation) and the MFCCs show a significant frame-by-frame correlation. The possible absence of correlation between the lower frequencies of abs(normalised autocorrelation) and the MFCCs is meaningless, as MFCCs emphasise the higher frequencies (cf part 2).
MFCCs part 4: intuitive interpretation of MFCCs
At this stage, we have a link between autocorrelation and MFCCs. To rephrase, MFCCs behave similarly to the part of autocorrelation that corresponds to higher frequencies. We are not far from a simple, intuitive interpretation of MFCCs.
MFCCs are the DCT of the resampled log(abs(FT)), in other words the DCT of the filtered log(abs(FT)). Therefore, as illustrated in Figure 13, if we convert the filter in the time domain, MFCCs are the DCT of the log(abs(FT)) of the filtered audio (using the converted filter).

Figure 13. DCT of filtered FT is similar to the DCT of the FT of the reconstructed audio.
We know how this (time domain) filtered audio sounds. It corresponds to the (frequency domain) filtered power spectrum. It’s the third audio example from video 1.
It can be deduced that MFCCs of an audio file can be interpreted as the high-pass filtered (gradual, > ca. 800Hz, rough estimation, see parts 1 and 2) file’s autocorrelation, musical pitch removed, and robust to bandwidth reduction.
In other words, MFCCs quantify the self-similarity of the high-pass filtered signal at different time scales (musical pitch removed, robust to bandwidth reduction).
The entire process is summarised in Figure 14.

Figure 14. DCT of filtered FFT is similar to the autocorrelation of reconstructed audio for the higher bands.
Figure 15 zooms on the most relevant part of Figure 14: the correlation between MFCCs and autocorrelation for the frequency bands in which the MFCC contains the most information.

Figure 15. MFCCs can be interpreted as autocorrelation of higher frequency bands, musical pitch removed, and robust to bandwidth reduction.
Conclusion: do MFCCs reflect “timbre”?
MFCCs quantify the self-similarity of the high-pass filtered signal at different time scales (musical pitch removed, robust to bandwidth reduction).
Given the success of MFCCs in the voice recognition task, it follows that human voices can be identified by the self-similarity of the high-pass filtered (gradual, above ca. 800Hz) signal at different time scales.
Does it mean that MFCCs can describe “timbre” in music?
It remains an open question. For instance, [Peeters et al., 2011] mention as part as the definition for “timbre”:
- The odd-to-even harmonic ratio. Such a feature will be set aside by the MFCC analysis, as a result of the blurring of pitch mentioned in part 2.
- The “tristimulus” values, which were introduced by [Pollard and Jansson, 1982] as a timbral equivalent to colour attributes in vision. The tristimulus comprises three different energy ratios allowing a fine description of the first harmonics of the spectrum. Such a feature will also be set aside by the MFCC analysis, as a result of both the blurring of pitch and emphasis on the higher frequencies mentioned in part 2 and deriving from the mel scale resampling of the spectrum.
Another aspect of timbre resides in acoustic beats. Two frequencies that are close to each other will generate a complex volume envelope that can’t be seen on the spectrogram. This phenomenon can be heard in music. For instance, power chords can result in acoustic beats if the guitar strings are not perfectly tuned — which might not be unfrequent in the music genre that features power chords (hard rock, metal…). Again, any information relevant to acoustic beats will be discarded from MFCC analysis, as a result of the blurring of pitch mentioned in part 2.
As cited in the introduction, [Mauch et. al, 2015] conclude that “[t]he decline in topic diversity and disparity [in popular music] in the early 1980s is due to a decline of timbral […] diversity”. We can now rephrase their conclusion: “we observed a decline of diversity in the patterns followed by the self-similarity of the high pass filtered signal at different time scales”.
Does it mean that “timbre” is getting more uniform? Again, it remains an open question.
Appendix: MFCC and topics in [Mauch et. al, 2015]
[Mauch et. al, 2015] describe “timbre” as follows. Largely quoting the original paper, the MFCCs used to measure timbre are discretized into ‘words’ resulting in a timbral lexicon (T-lexicon) of timbre clusters. To relate the T-lexicon to semantic labels in plain English, they carried out expert annotations. The musical words from the lexicon were then combined into eight ‘topics’ using Latent Dirichlet Allocation (LDA). LDA is a hierarchical generative model of a text-like corpus, in which every document (here: song) is represented as a distribution over a number of topics, and every topic is represented as a distribution over all possible words (here: timbre clusters from the T-lexicon). Each song, then, is represented as a distribution over eight timbral topics (T-topics) that capture particular timbres (e.g. ‘drums, aggressive, percussive’, ‘female voice, melodic, vocal’, derived from the expert annotations), with topic proportions q. These topic frequencies were the basis of the analysis.
References
[Mauch et. al, 2015] Mauch, Matthias, et al. “The evolution of popular music: USA 1960–2010.” Royal Society open science 2.5 (2015): 150081.
[Muda et al., 2010] Muda, Lindasalwa, Mumtaj Begam, and Irraivan Elamvazuthi. “Voice recognition algorithms using mel frequency cepstral coefficient (MFCC) and dynamic time warping (DTW) techniques.” arXiv preprint arXiv:1003.4083 (2010).
[Peeters et al., 2011] Peeters, Geoffroy, et al. “The timbre toolbox: Extracting audio descriptors from musical signals.” The Journal of the Acoustical Society of America 130.5 (2011): 2902–2916.
[Pollard and Jansson, 1982] Pollard, Howard F., and Erik V. Jansson. “A tristimulus method for the specification of musical timbre.” Acta Acustica united with Acustica 51.3 (1982): 162–171.
[Yu and Deng, 2016] Yu, Dong, and Li Deng. Automatic speech recognition. Vol. 1. Berlin: Springer, 2016.