đŸȘŽ Anil's Garden

Gram-Schmidt process

10 Feb 20256 min read

The Gram-Schmidt process (or procedure) is a sequence of operations that allow us to transform a set of linearly independent vectors into a set of orthonormal vectors that span the same space spanned by the original set.

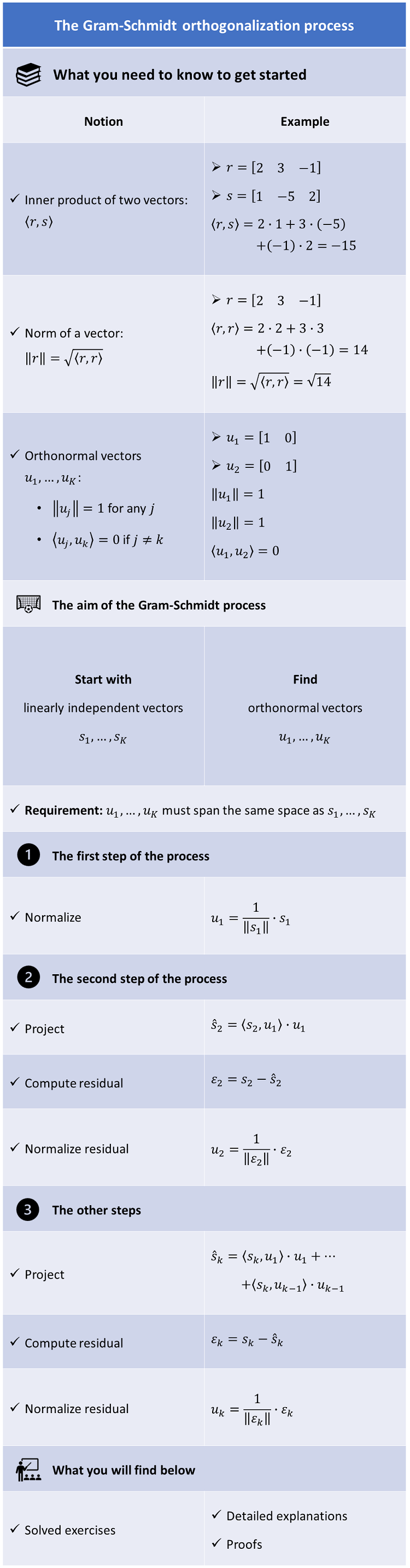
Infographic summarizing the main steps of the Gram-Schmidt orthogonalization algorithm.

Table of Contents

Table of contents

  1. Preliminaries

  2. Projections on orthonormal sets

  3. Normalization

  4. Overview of the procedure

  5. Formal statement

  6. Every inner product space has an orthonormal basis

  7. Solved exercises

  8. Exercise 1

  9. Exercise 2

Preliminaries

Let us review some notions that are essential to understand the Gram-Schmidt process.

Remember that two vectors r and s are said to be orthogonal if and only if their inner product is equal to zero, that is,[eq1]

Given an inner product, we can define the norm (length) of a vector s as follows:[eq2]

A set of vectors is called orthonormal if and only if its elements have unit norm and are orthogonal to each other. In other words, a set of K vectors [eq3] is orthonormal if and only if[eq4]

We have proved that the vectors of an orthonormal set are linearly independent.

When a basis for a vector space is also an orthonormal set, it is called an orthonormal basis.

Projections on orthonormal sets

In the Gram-Schmidt process, we repeatedly use the next proposition, which shows that every vector can be decomposed into two parts: 1) its projection on an orthonormal set and 2) a residual that is orthogonal to the given orthonormal set.

Proposition Let S be a vector space equipped with an inner product [eq5]. Let [eq6] be an orthonormal set. For any sin S, we have[eq7]where varepsilon _{S} is orthogonal to u_{k} for any k=1,ldots ,K.

Proof

The term[eq11]is called the linear projection of s on the orthonormal set [eq12], while the term varepsilon _{S} is called the residual of the linear projection.

Normalization

Another perhaps obvious fact that we are going to repeatedly use in the Gram-Schmidt process is that, if we take any non-zero vector and we divide it by its norm, then the result of the division is a new vector that has unit norm.

In other words, if [eq13] then, by the definiteness property of the norm, we have that [eq14]

As a consequence, we can define[eq15]and, by the positivity and absolute homogeneity of the norm, we have[eq16]

Overview of the procedure

Now that we know how to normalize a vector and how to decompose it into a projection on an orthonormal set and a residual, we are ready to explain the Gram-Schmidt procedure.

We are going to provide an overview of the process, after which we will express it formally as a proposition and we will discuss all the technical details in the proof of the proposition.

Here is the overview.

We are given a set of linearly independent vectors [eq17].

To start the process, we normalize the first vector, that is, we define[eq18]

In the second step, we project s_{2} on u_{1}:[eq19]where varepsilon _{2} is the residual of the projection.

Then, we normalize the residual:[eq20]

We will later prove that [eq21] (so that the normalization can be performed) because the starting vectors are linearly independent.

The two vectors u_{1} and u_{2} thus obtained are orthonormal.

In the third step, we project s_{3} on u_{1} and u_{2}:[eq22]and we compute the residual of the projection varepsilon _{3}.

We then normalize it:[eq23]

We proceed in this manner until we obtain the last normalized residual u_{K} .

At the end of the process, the vectors [eq24] form an orthonormal set because:

  1. they are the result of a normalization, and as a consequence they have unit norm;
  2. each u_{k} is obtained from a residual that has the property of being orthogonal to [eq25].

To complete this overview, let us remember that the linear span of [eq17] is the set of all vectors that can be written as linear combinations of [eq17]; it is denoted by[eq28]and it is a linear space.

Since the vectors [eq29] are linearly independent combinations of [eq17], any vector that can be written as a linear combination of [eq17] can also be written as a linear combination of [eq29]. Therefore, the spans of the two sets of vectors coincide:[eq33]

Formal statement

We formalize here the Gram-Schmidt process as a proposition, whose proof contains all the technical details of the procedure.

Proposition Let S be a vector space equipped with an inner product [eq5]. Let [eq35] be linearly independent vectors. Then, there exists a set of orthonormal vectors [eq36] such that[eq37]for any kleq K.

Proof

The proof is by induction: first we prove that the proposition is true for k=1, and then we prove that it is true for a generic k if it holds for k-1. When k=1, the vector[eq18]has unit norm and it constitutes by itself an orthonormal set: there are no other vectors, so the orthogonality condition is trivially satisfied. The set[eq39]is the set of all scalar multiples of s_{1}, which are also scalar multiples of u_{1} (and vice versa). Therefore, [eq40]Now, suppose that the proposition is true for k-1. Then, we can project s_{k} on [eq41]:[eq42]where the residual varepsilon _{k} is orthogonal to [eq43]. Suppose that varepsilon _{k}=0. Then,[eq44]Since, by assumption, [eq45]for any jleq k-1, we have that [eq46]for any jleq k-1, where alpha _{jl} are scalars. Therefore,[eq47]In other words, the assumption that varepsilon _{k}=0 leads to the conclusion that s_{k} is a linear combination of [eq48]. But this is impossible because one of the assumptions of the proposition is that [eq17] are linearly independent. As a consequence, it must be that [eq50]. We can therefore normalize the residual and define the vector[eq51]which has unit norm. We already know that varepsilon _{k} is orthogonal to [eq52]. This implies that also u_{k} is orthogonal to [eq53]. Thus, [eq54] is an orthonormal set. Now, take any vector sin S that can be written as[eq55]where [eq56] are scalars. Since, by assumption, [eq57]we have that equation (2) can also be written as[eq58]where [eq59] are scalars, and: in step frame{A} we have used equation (1); in step frame{B} we have used the definition of u_{k}. Thus, we have proved that every vector that can be written as a linear combination of [eq60] can also be written as a linear combination of [eq54]. Assumption (3) allows us to prove the converse in a completely analogous manner:[eq62]In other words, every linear combination of [eq54] is also a linear combination of [eq64]. This proves that [eq37]and concludes the proof.

Every inner product space has an orthonormal basis

The following proposition presents an important consequence of the Gram-Schmidt process.

Proposition Let S be a vector space equipped with an inner product [eq5]. If S has finite dimension [eq67], then there exists an orthonormal basis [eq68] for S.

Proof

Solved exercises

Below you can find some exercises with explained solutions.

Exercise 1

Consider the space S of all 3 imes 1 vectors having real entries and the inner product[eq74]where r,sin S and s^{ op } is the transpose of s.

Define the vector[eq75]

Normalize s.

Solution

The norm of s is[eq76]Therefore, the normalization of s is[eq77]

Exercise 2

Consider the space S of all 2 imes 1 vectors having real entries and the inner product[eq78]where r,sin S .

Consider the two linearly independent vectors[eq79]

Transform them into an orthonormal set by using the Gram-Schmidt process.

Solution

The norm of s_{1} is [eq80]Therefore, the first orthonormal vector is[eq81]The inner product of s_{2} and u_{1} is[eq82]The projection of s_{2} on u_{1} is[eq83]The residual of the projection is[eq84]The norm of the residual is[eq85]and the normalized residual is[eq86]Thus, the orthonormal set we were looking for is[eq87]

How to cite

Please cite as:

Taboga, Marco (2021). “Gram-Schmidt process”, Lectures on matrix algebra. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

Invitation to consider a paper textbook as a complement to a digital textbook

Graph View

Backlinks