Self-Supervised Visual Representation Learning

This post consolidates several literature summaries from the field of self-supervised visual representation learning.

---

• MoCo: Momentum Contrast for Unsupervised Visual Representation Learning
  • Introduction
  • Contrastive Learning as Dictionary Look-up
  • Key Ideas: Momentum and the Queue of Keys
  • Algorithm
  • Shuffling Batch Norm: Batch Normalisation Leaking Information
  • What is the Dictionary Queue
  • Details
  • Comparison to Previous Self-Supervised Approaches
  • Implementation
• SimSiam: Exploring Simple Siamese Representation Learning
  • Key Points
  • Background and Lead-in
  • Contributions
  • Method
  • Stop-gradient
  • Predictor “Head”
  • Batch Size
  • Batch Norm
  • Similarity Function
  • Symmetrization
  • Hypothesis
  • Additional
  • Implementation
• BYOL: Bootstrap Your Own Latent A New Approach to Self-Supervised Learning
  • Summary from Papers with Code
  • Key Points
  • Background
• UVC: Joint-task Self-supervised Learning for Temporal Correspondence
  • Introduction
  • Related Work
  • Approach
  • Transforming Feature and Location via Affinity
  • Interesting References
• SwAV: Unsupervised Learning of Visual Features by Contrasting Cluster Assignments
  • Summary of Contributions
  • Core Explanations from the FAIR Post
  • Related Work
  • Method
• VFS: Rethinking Self-supervised Correspondence Learning A Video Frame-level Similarity Perspective
  • Summary
  • Main Results
  • Approach
  • Results
  • Additional Notes
  • Authors’ Conclusions
  • Implementation

---

---

SimSiam: Exploring Simple Siamese Representation Learning

Notes on SimSiam: Exploring Simple Siamese Representation Learning by Xinlei and Chen Kaiming He.

• Paper: https://arxiv.org/pdf/2011.10566.pdf
• Code: https://github.com/facebookresearch/simsiam
• Papers with Code: https://paperswithcode.com/paper/exploring-simple-siamese-representation

The background and perspectives work this paper provides is a treasure trove. The point of the paper is, in many ways, to unify the perspectives brought to the table by a selection of landmark SSL vision papers (from large organisations), in particular SimCLR, MoCo, SwAV and BYOL.

Key Points

Abstract restructured

Siamese networks have become a common structure in various recent models for unsupervised visual representation learning. These models maximize the similarity between two augmentations of one image, subject to certain conditions for avoiding collapsing solutions.

In this paper, we report surprising empirical results that simple Siamese networks can learn meaningful representations even using none of the following:

1. negative sample pairs
2. large batches
3. momentum encoders

Our experiments show that collapsing solutions do exist for the loss and structure, but a stop-gradient operation plays an essential role in preventing collapsing.

We provide a hypothesis on the implication of stop-gradient, and further show proof-of-concept experiments verifying it.

Our “SimSiam” method achieves competitive results on ImageNet and downstream tasks.

We hope this simple baseline will motivate people to rethink the roles of Siamese architectures for unsupervised representation learning.

Background and Lead-in

• Siamese networks are parallel networks with weight sharing, so can be more practically thought of as training set-ups / paradigms where the forward pass is conducted twice with different inputs, whether these come from the same image as two different “views” (also called “augmentations” or “transformations”) or different inputs (as in the supervised setting).
• They are used for comparing entities and are used for signature and face verification, tracking, one-shot learning with inputs usually being different images and supervision used for training.
• Siamese networks are used for contrastive learning where a contrastive loss attracts similar samples and repels dissimilar ones, which can in turn be used for SSL when the positive samples are from the same image and negative samples from different images. (Not just images.)
  • Large number of negative samples improve training of the encoder backbone being SS trained
  • MoCo maintains a queue of a large number of negative samples
  • SimCLR uses a large number of negative samples inside the batch; and therefore requires very large (e.g. 4096) batch size
• Clustering-based methods alternate between cluster assignment of samples to act as pseudolabels, and training using those assignments.
  • SwAV does clustering with a Siamese Network where one forward pass computes the cluster assignment and the other pass predicts the assignment from another view (we say predicts because that other view is given the features, and the loss is taken between cluster assignments and features, at least from what I understand of the paper at this point)
  • SwAV does this online - i.e. does not alternate between cluster assignment and training with cluster pseudolabels by satisfying an equipartition constraint within batches (so batches need to be big enough, e.g. 256; or else using information from previous batches / iterations)
  • SwAV solves the equipartition constraint (i.e. the transportation polytope) via the Sinkhorn-Knopp transform (see Sinkhorn Distances: Lightspeed Computation of Optimal Transport by Marco Cuturi published in 2013 at NIPS)
• Clustering-based SSL methods use clusters as negative prototypes instead of explicitly using negative samples
• Clustering-based SSL methods require large batches, a memory bank or a queue to provide enough (negative) samples for clustering
• BYOL directly predicts the output of one view from another view using a momentum encoder for one branch, which the authors hypothesise is important to avoid collapse¹

Contributions

• The authors find that the momentum-encoder is not required to avoid collapse but rather a stop-gradient, which is confounded with the momentum-encoder since a stop-gradient is required for one²
  • Note: A momentum-encoder might still improve accuracy for a correctly-tuned momentum value, $m$

Method

• Take two randomly augmented views, $x_1$ and $x_2$, from an image $x$
• Pass these two views through the forward pass of an encoder and projection head (e.g. ResNet followed by MLP)
• The encoder, $f$, implements weight sharing
• A projection head, $h$ transforms the output of one view and matches it to another view
• We have the two outputs from the input views: $p_1\triangleq h(f(x_1))\triangleq h(z_1)$ and $z_2=f(x_2)$
• The negative cosine similarity is used as a minimisation criterion, which is equivalent to the MSE of the $l_2$-normalised vectors up to a scaling coefficient of 2

$\mathcal{D}\left(p_1,z_2\right)=-\frac{p_1}{\Vert p_1{\Vert }_2}\cdot \frac{z_2}{\Vert z_2{\Vert }_2}$

• The overall loss is a “symmetrized loss” composed of the average of the two negative cosine similaries that take the output with and without the projection head (i.e. from the two branches of the network) in each case

$\mathcal{L}=\frac{1}{2}\mathcal{D}\left(p_1,z_2\right)+\frac{1}{2}\mathcal{D}\left(p_2,z_1\right)$

• The average loss is taken over the images (in a minibatch) with the minimum possible loss being $-1$

**The crucial stop-gradient operation operation is implemented by modifying the negative cosine similarity function to:

$\mathcal{D}({\mathbf{p}}_1,\mathrm{stopgrad}({\mathbf{z}}_2))$

This means that $z_2$ is treated as a constant in this term

In other words, no gradient flows back from $z_2$ in this component of the loss (in the full loss, there is also the other component). The overall, stop-gradient-modified loss is:

$\mathcal{L}=\frac{1}{2}\mathcal{D}(p_1,\mathrm{stopgrad}(z_2))+\frac{1}{2}\mathcal{D}(p_2,\mathrm{stopgrad}(z_1)$

Keep in mind that z_\text{view_idx} stands for the network output without (or I guess “before”) the projection head and p_\text{view_idx} stands for the network output with the projection head.

So we have no gradient backpropagation from the no-MLP (pre-projection) output in the first term and no gradient backpropagation from the no-MLP output in the second term. Note: In this set-up, we’re always stopping the gradient flowing back from the pre-projection vectors outputs of the network.

{:refdef: style=“text-align: center;“} {: refdef}

Details

• SGD - they don’t used LARS
  • SGD momentum is 0.9
• Learning Rate = Batch Size / 256 (linear scaling) with base learning rate of $0.05$.
  • Learning rate has cosine decay schedule
  • Weight decay is 1e-4 or $10^{-4}$
• Batch size is 512 by default (using 8 GPUs), but you can vary it
• They use Batch Normalisation synchronised across devices
• Projection MLP, which is part of $f$, is a three-layer MLP (hidden FC is 2048-D) with BN each layer and ReLU apart from the output layer
• Prediction MLP, $h$, is a two-layer MLP with BN on all hidden layers except the output, which also doesn’t have a ReLU
  • Input and output dimensions are equal at 2048
  • Hidden layer dimension is 512
• ResNet-50 is the default backbone
• 100 epoch pretraining is reported for ablations
• Self-supervised pretraining on 1,000-class ImageNet training without labels
• Linear evaluation protocol used; this is used on validation set
  • this is the same evaluation protocol everyone uses and reports e.g. SwAV

Note: $h$ is a bottleneck structure since its hidden layer dimension is 512 versus the input and output dimensionalities of 2048.

Stop-gradient

{:refdef: style=“text-align: center;“} {: refdef}

Above is Figure 2 from the paper, which compares performance (behaviour really) with and without the stop-gradient.

Left: Training loss becomes $-1$ (its minimum) almost immediately without the stop gradient indicative that collapse has occurred, as the model has found the trivial solution.

Middle: The standard deviation of $l\_2$-normalised pre-projection head network outputs: $\mathrm{std}(z/\Vert z{\Vert }_2)$. If encoded vectors collapse to the same output representation there will be no variation in the network outputs, so the standard deviation will be zero. This is the value shown without the stop-gradient.

By contrast, in blue is shown the standard deviation of $l_2$-normalised output representations with the stop-gradient, which are around $1/\sqrt{d}$ where $d$ is the output vector dimensionality; this is the value expected under a zero-mean isotropic Gaussian distribution.

This indicates there is not collapse, and in fact the outputs are distributed along the unit hypersphere, which is basically a fancy way of saying they’re multivariate normally distributed with variance one in $d$-dimensional space. (This also sounds too fancy for my liking, but it’s the best I got right now.)

Right: k-Nearest Neighbour accuracy which serves as a metric for the downstream performance of the encoder is consistently close to zero without stop-gradient and steadily improves with it.

Headline Result: SimSiam achieves accuracy on ImageNet validation via the linear evaluation protocol of 67.7% which drops to 0.1% (the chance level) without the stop-gradient.

Collapsing solutions exist, indicated by minimum possible loss and the constant outputs (low kNN accuracy is an insufficient indicator, since diverging loss can also cause poor kNN accuracy). These cannot be avoided by architecture design along (e.g. BN, adding a predictor MLP, normalisation).

Something else is going on: another optimisation problem is being solved by the stop-gradient in the Siamese network. (See Hypotheis.)

Predictor “Head”

• The model doesn’t work without the predictor MLP (if it is an identity mapping)

Concretely, this makes the loss

$\mathcal{L}=\frac{1}{2}\mathcal{D}(z_1,\mathrm{stopgrad}(z_2))+\frac{1}{2}\mathcal{D}(z_2,\mathrm{stopgrad}(z_1)$

i.e. we replace the p_\text{view_idx} terms with the no-Predictor z_\text{view_idx} terms.

• It seems like there is a crucial role of the predictor in decoupling the gradients produced in backpropagation of the with-Predictor branch from the no-Predictor branch, indeed by decoupling the network branches (making them non-equivalent).
• Think: Removing the Predictor head makes he two branches equal and makes the loss symmetric, so all you are doing is rescaling the gradients (the magnitude of the gradient vectors) by $\frac{1}{2}$.
  • This in turn allows the network to update to the trivial soluiton, albeit taking twice as long (twice as many updates) to do so
• We’re talking about the loss that they made symmetric, but empirically, the authors found the network collapses with the asymmetric loss as well without the Predictor head.
• Note: BYOL also uses an asymmetric pair of network branches, one of which has a Predictor and the other that does not
• The network does not converge if $h$ is fixed with randomly initialised weights
• Predictor head, $h$, with constant learning rate yields better performance than with lr decay

Here’s the Predictor Head in the SimSiam model (Module) class:

# build a 2-layer predictor
self.predictor = nn.Sequential(nn.Linear(dim, pred_dim, bias=False),
                                nn.BatchNorm1d(pred_dim),
                                nn.ReLU(inplace=True), # hidden layer
                                nn.Linear(pred_dim, dim)) # output layer

Batch Size

• They tried batch sizes 64 to 4096
• They kept linear scaling of lr (lr $\times$ batch size / 256)
• Evne with batch sizes of 128 or 64 they maintain high accuracy (drop are ~0.8% or 2.0%)
• SimCLR and SwAV are true Siamese Networks but require large batch sizes
• Large batch sizes hurt performance, possibly because they didn’t use LARS (they stuck with SGD)

Take home point: SimSiam does not require large batch sizes.

Batch Norm

• Removing BN from MLP heads hurts performance (34.6%) but does not collapse
  • Performance hit is just optimisation difficulty
  • Adding BN to hidden layers restores it to 67.4%
• Adding BN to output of encoder’s projection MLP (i.e. the one that goes over the output of $f$) boosts performance to 68.1%
• You don’t need the learnable affine transformation of the Batch Norm layers: 68.2% accuracy without these learnable Batch Norm layer parameters.
  • Note the nn.BatchNorm1d(dim, affine=False) # output layer in the encoder.fc of the SimSiam Module
• BN on the Predictor MLP causes loss to oscillate and hurts performance

Overall: BN behaves like it does in supervised settings and cannot itself prevent collapse.

Just for reference, here’s the whole projection head of the encoder of the SimSiam model class.

# build a 3-layer projector
prev_dim = self.encoder.fc.weight.shape[1]
self.encoder.fc = nn.Sequential(nn.Linear(prev_dim, prev_dim, bias=False),
                                nn.BatchNorm1d(prev_dim),
                                nn.ReLU(inplace=True), # first layer
                                nn.Linear(prev_dim, prev_dim, bias=False),
                                nn.BatchNorm1d(prev_dim),
                                nn.ReLU(inplace=True), # second layer
                                self.encoder.fc,
                                nn.BatchNorm1d(dim, affine=False)) # output layer
self.encoder.fc[6].bias.requires_grad = False # hack: not use bias as it is followed by BN

Similarity Function

The similarity function is not responsible for the observed behaviour (ablation).

• Swapping out the negative cosine similarity for the cross-entropy similarity (made symmetric for the loss in the same way as before) leads to the same scenario where collapse occurs without stop-gradient
• Accuracy is lower with the cross-entropy similarity: 63.2% (c.f. 68.1%)

You swap out $\mathcal{D}$ to be this

$\mathcal{D}\left(p_1,z_2\right)=-\mathrm{softmax}(z_2)\cdot \log \mathrm{softmax}(p_1)$

The softmax is taken along the channel dimension, so it is a distribution amongst $d$ pseudo-categories.

This sets up some connection to SwAV (which uses pseudocategories - their clusters - for its contrastive loss).

Symmetrization

• The asymmetric loss, i.e. just $\mathcal{D}$ applied one way, damages performance slightly but is not responsible for preventing collapse
  • Performance stays around 64.8% or 67.3% if you sample two image pairs (to account for what you are effectively doing in the symmetric loss)

Hypothesis

We have empirically shown that in a variety of settings, SimSiam can produce meaningful results without collapsing. The optimizer (batch size), batch normalization, similarity function, and symmetrization may affect accuracy, but we have seen no evidence that they are related to collapse prevention. It is mainly the stop-gradient operation that plays an essential role.

A hypothesis on what is implicitly optimized by SimSiam, with proof-of-concept experiments from the authors follows.

Section coming soon

Additional

Some extra bits.

What is a cosine learning rate schedule

Also called Cosine Annealing, a cosine learning rate schedule is a…

…type of learning rate schedule that has the effect of starting with a large learning rate that is relatively rapidly decreased to a minimum value before being increased rapidly again.

The resetting of the learning rate acts like a simulated restart of the learning process and the re-use of good weights as the starting point of the restart is referred to as a “warm restart” in contrast to a “cold restart” where a new set of small random numbers may be used as a starting point.

Source: Cosine Annealing entry on Papers with Code.

First introduced in SGDR: Stochastic Gradient Descent with Warm Restarts by Ilya Loshchilov and Frank Hutter in 2016

Why is this is the value expected under a zero-mean isotropic Gaussian distribution?

• For an output vector, $z$, we have its $l_2$-normalised counterpart $z^{\prime }\triangleq z/\Vert z{\Vert }_2$.
• So for an element of that vector, i.e. the $i$th channel, after normalisation we have $z_i^{\prime }=z_i/sqrt{\sum }_{j=1}^d{z}_j^2)$³.
• If we have elements (in channels) normally distributed with mean zero and standard deviation one, $z_j\sim \mathcal{N}(0,1)\forall j$
• Then we have $d\times$ variance equal to the term inside the summation inside the square root in the denominator: $z_j^2$ since this is the average squared distance from the mean (remember the mean is zero)
• We sum this variance, which we said was $1$ in the Gaussian, $d$ times ${\sum }_{j=1}^d{z}_j^2$
• Finally, we square root it
• So it makes sense then that we have have elements after normalisation $z_i^{\prime }\approx z_i/\sqrt{d}$
• And the standard deviation of these elements is the same distance away from zero, but now also scaled: $1/\sqrt{d}$

Implementation

import torch
import torch.nn as nn
 
 
class SimSiam(nn.Module):
    """
    Build a SimSiam model.
    """
    def __init__(self, base_encoder, dim=2048, pred_dim=512):
        """
        dim: feature dimension (default: 2048)
        pred_dim: hidden dimension of the predictor (default: 512)
        """
        super(SimSiam, self).__init__()
 
        # create the encoder
        # num_classes is the output fc dimension, zero-initialize last BNs
        self.encoder = base_encoder(num_classes=dim, zero_init_residual=True)
 
        # build a 3-layer projector
        prev_dim = self.encoder.fc.weight.shape[1]
        self.encoder.fc = nn.Sequential(nn.Linear(prev_dim, prev_dim, bias=False),
                                        nn.BatchNorm1d(prev_dim),
                                        nn.ReLU(inplace=True), # first layer
                                        nn.Linear(prev_dim, prev_dim, bias=False),
                                        nn.BatchNorm1d(prev_dim),
                                        nn.ReLU(inplace=True), # second layer
                                        self.encoder.fc,
                                        nn.BatchNorm1d(dim, affine=False)) # output layer
        self.encoder.fc[6].bias.requires_grad = False # hack: not use bias as it is followed by BN
 
        # build a 2-layer predictor
        self.predictor = nn.Sequential(nn.Linear(dim, pred_dim, bias=False),
                                        nn.BatchNorm1d(pred_dim),
                                        nn.ReLU(inplace=True), # hidden layer
                                        nn.Linear(pred_dim, dim)) # output layer
 
    def forward(self, x1, x2):
        """
        Input:
            x1: first views of images
            x2: second views of images
        Output:
            p1, p2, z1, z2: predictors and targets of the network
            See Sec. 3 of https://arxiv.org/abs/2011.10566 for detailed notations
        """
 
        # compute features for one view
        z1 = self.encoder(x1) # NxC
        z2 = self.encoder(x2) # NxC
 
        p1 = self.predictor(z1) # NxC
        p2 = self.predictor(z2) # NxC
 
        return p1, p2, z1.detach(), z2.detach()

---

BYOL: Bootstrap Your Own Latent A New Approach to Self-Supervised Learning

Notes on Bootstrap Your Own Latent A New Approach to Self-Supervised Learning by Jean-Bastien Grill et al.

• Paper: https://arxiv.org/pdf/2006.07733.pdf
• Code (JAX): https://github.com/deepmind/deepmind-research/tree/master/byol and ByolExperiment model class
• Code (PyTorch): https://github.com/lucidrains/byol-pytorch with BYOL model class
• Papers with Code: https://paperswithcode.com/method/byol

Summary from Papers with Code

BYOL (Bootstrap Your Own Latent) is a new approach to self-supervised learning. BYOL’s goal is to learn a representation $y_{\theta }$ which can then be used for downstream tasks. BYOL uses two neural networks to learn: the online and target networks. The online network is defined by a set of weights $\theta$ and is comprised of three stages: an encoder $f_{\theta }$, a projector $g_{\theta }$ and a predictor $q_{\theta }$. The target network has the same architecture as the online network, but uses a different set of weights $\xi$. The target network provides the regression targets to train the online network, and its parameters $\xi$ are an exponential moving average of the online parameters $\theta$.

Given the architecture diagram [below], BYOL minimizes a similarity loss between $q_{\theta }\left(z_{\theta }\right)$ and $sg\left(z_{\xi }^{\prime }\right)$, where $\theta$ are the trained weights, $\xi$ are an exponential moving average of $\theta$ and $sg$ means stopgradient. At the end of training, everything but $f_{\theta }$ is discarded, and $y_{\theta }$ is used as the image representation.

{:refdef: style=“text-align: center;“} 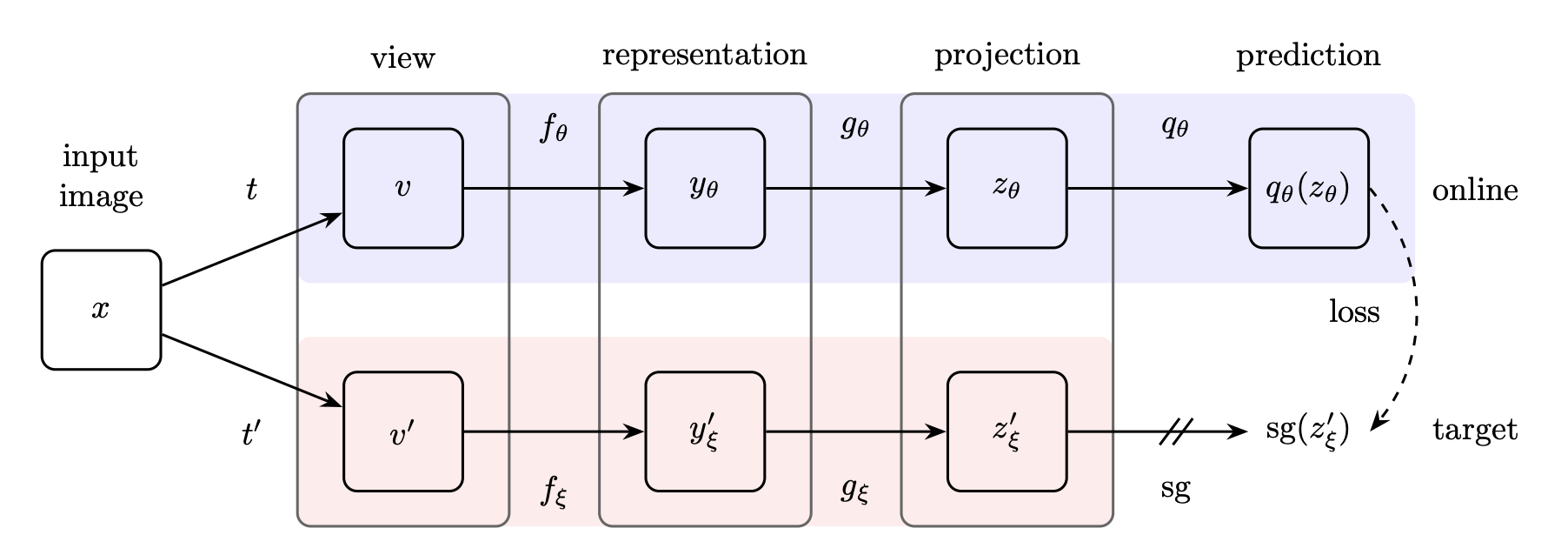{: refdef}

Key Points

• With parallel online and target networks, they train the online network given one augmented view to predict the target network representation given another view, directly
• BYOL does not use any negative pairs (negative samples)
  • Note the lack of mention of any other images in the previous bullet point: just two views of the same image
• More robust over augmentations and variations in batch size than methods which use (explicit?) negative pairs (including if those negative samples are somehow transformed, e.g. in the case of clustering-based SSL like DeepCluster)
  • In particular, BYOL suffers a much smaller performance drop than SimCLR, a strong contrastive baseline, when only using random crops as image augmentations (quoted from Introduction)
• BYOL gets 74.3% accuracy on the ImageNet linear evaluation protocol with a ResNet-50 encoder⁴
• BYOL is good for transfer and semi-supervised downstream stuff

This paper was published after MoCo (and in fact cites it; see ref [9]) but its contribution is eliminating the negative samples that are still used by approaches like e.g. MoCo (which uses a queue of negative samples).

Background

Self-supervised methods are generative - like auto-encoding or adversarial learning - or discriminative - like contrastive learning with positive and negative samples.

They enumerate the many domain-specific pretext tasks that people tried out before contrastive methods appeared as the key paradigm for self-supervised learning:

Some self-supervised methods are not contrastive but rely on using auxiliary handcrafted prediction tasks to learn their representation. In particular, relative patch prediction [23, 40], colorizing gray-scale images [41, 42], image inpainting [43], image jigsaw puzzle [44], image super-resolution [45], and geometric transformations [46, 47] have been shown to be useful. Yet, even with suitable architectures [48], these methods are being outperformed by contrastive methods [37, 8, 12].

They mention similarity with Predictions of Bootstrapped Latents (PBL) from Bootstrap Latent-Predictive Representations for Multitask Reinforcement Learning, which trains its representation by predicting latent embeddings of future observations (see PBL Abstract). (BYOL doesn’t use a second network like PBL; it uses a momentum encoder.)

They say that using a slow-moving (e.g. momentum) encoder to encode targets comes from deep RL, citing e.g. Human-level control through deep reinforcement learning (see also references [50-53]) saying that:

Target networks stabilize the bootstrapping updates provided by the Bellman equation … [but w]hile most RL methods use fixed target networks, BYOL uses a weighted moving average of previous networks (as in [54]) in order to provide smoother changes in the target representation.

BYOL introduces an additional predictor on top of the online network, which prevents collapse.

Whereas MoCo drawn negative samples from its queue, BYOL just uses a moving-average encoder to produce prediction targets to prevent collapse.

---

A Note on Citations

This paper seems to do a good job of citing the work it has built on. They reference Reinforcement Learning literature (a lot from DeepMind 🤔) but also older work like Suzanna Becker and Geoffrey E. Hinton (1992) Self-organizing neural network that discovers surfaces in random-dot stereograms. Nature, which was a nice discovery when chasing up these references.

---

UVC: Joint-task Self-supervised Learning for Temporal Correspondence

Notes on Joint-task Self-supervised Learning for Temporal Correspondence (UVC) by Xueting Li and colleagues published in 2019.

• Paper: https://arxiv.org/pdf/1909.11895.pdf
• Code: https://github.com/Liusifei/UVC

Introduction

• correspondences between multi-view images relate 2D and 3D representations
• To learn correspondences across frames in a video, numerous methods have been developed from two perspectives: (a) learning region/object-level correspondences, via object tracking [2, 41, 43, 36, 48] or (b) learning pixel-level correspondences between multi-view images or frames, e.g., via stereo matching [34] or optical flow estimation [29, 40, 16, 31]
• not solved together
• Different annotations: bounding boxes are annotated in real videos for object tracking [52]; and pixel-wise associations are generated from synthesized data for optical flow estimation [4, 10]. Datasets with annotations for both tasks are scarcely available and supervision, here, is a further bottleneck preventing us from connecting the two tasks.
• Method: To overcome the lack of data with annotations for both tasks we exploit self-supervision via the signals of
  • (a) Temporal Coherency, which states that objects or scenes move smoothly and gradually over time;
  • (b) Cycle Consistency, correct correspondences should ensure that pixels or regions match bi-directionally and
  • (c) Energy Preservation, which preserves the energy of feature representations during transformations
• Share affinity matrix for obj- and pixel-features
• We show that region localization and fine-grained matching can be carried out by sharing the affinity in a fully differentiable manner
• two tasks symbiotically facilitate each other: the fine-grained matching module learns better feature representations that lead to an improved affinity matrix, which in turn generates better localization that reduces the search space and ambiguities for fine-grained matching (Figure 1, right)
• Contributions:
  • A joint-task self-supervision network is introduced to find accurate correspondences at different levels across video frames
  • A general inter-frame transformation is proposed to support both tasks and to satisfy various video constraints: coherency, cycle, and energy consistency
• Our method outperforms state-of-the-art methods on a variety of visual correspondence tasks, e.g., video instance and part segmentation, keypoints tracking, and object tracking. Our self-supervised method even surpasses the fully-supervised affinity feature representation obtained from a ResNet-18 pre-trained on the ImageNet

Related Work

• Object-level correspondence: Our work can be viewed as exploiting the tracking-by-matching framework in a self-supervised manner
• Fine-grained correspondence:
  • Dense correspondence between video frames has been widely applied for optical flow and motion estimation [31, 40, 29, 16], where the goal is to track individual pixels
  • Deep optical flow mostly regresses optical flows
  • direct regression of pixel offsets has limited capability for frames containing dramatic appearance changes
• Self-supervised learning: Recently, numerous approaches have been developed for correspondence learning via various self-supervised signals, including
  • image transformation[17]
  • color transformation [44]
  • cycle-consistency
    • Wang, Jabri and Efros (2019) Learning correspondence from the cycle-consistency of time. CVPR - develops patch-level tracking by modeling the similarity transformation of pixels within a fixed rectangular region
    • Wang et al. (2019) Unsupervised deep tracking. CVPR - correlation filter is learned to track regions via a cycle-consistency constraint, and no pixel-level correspondence is determined
• In contrast, our method learns object-level and pixel-level correspondence jointly across video frames in a self-supervised manner.

Approach

• You can think of frames as copies one-to-another with motion augmentation
• This “copy” operator can be expressed via a linear transformation with a matrix $A$, in which $A_{ij}=1$ denotes that the pixel $j$ in the second frame is copied from pixel $i$ in the first one. An approximation of $A$ is the inter-frame affinity matrix [43, 30, 51]:

$A_{ij}=\kappa \left(f_{1i},f_{2j}\right)$

where $\kappa$ denotes some similarity function. Each entry $A_{ij}$ represents the similarity of subspace pixels $i$ and $j$ in the two frames $f_1\in {\mathcal{R}}^{C\times N_1}$ and $f_2\in {\mathcal{R}}^{C\times N_2}$, where $f\in {\mathcal{R}}^{C\times N}$ is a vectorized feature map with $C$ channels and $N$ pixels. In this work, our goal is to learn the feature embedding $f$ that optimally associates the contents of the two frames.

• they utilize color as a “free supervisory signal”:
  • To learn the inter-frame transformation in a self-supervised manner, we can slightly modify $A_{ij}=\kappa \left(f_{1i},f_{2j}\right)$ to generate the affinity via features $f$ learned only from gray-scale images
  • the learned affinity is then utilized to map the color channels from one frame to another [44, 30], while using the ground-truth color as the self-supervisory signal

Problems

• One strict assumption of this formulation is that the paired frames need to have the same contents no new object or scene pixel should emerge over time
• Hence, the existing methods [44, 30] sample pairs of frames either uniformly, or randomly within a specified interval, e.g., 50 frames
• However, it is difficult to determine a “perfect” interval as video contents may change sporadically
• When transforming color from a reference frame to a target one, the objects/scene pixels in the target frame may not exist in the reference frame, thereby leading to wrong matches and an adverse effect on feature learning
• Another issue is that a large portion of the video frames are “static”, in which the sampled pair of frames are almost the same and cause the learned affinity to be an identity matrix

Solution: Incorporate a region-level localization module

• Given a pair of reference and target frames, we first randomly sample a patch in the reference frame and localize this patch in the target frame
• Interframe colour transformation is estimated between the paired patches
• Both localization and color transformation are supported by a single affinity derived from a convolutional neural network (CNN) based on the fact that the affinity matrix can simultaneously track locations and transform features

Transforming Feature and Location via Affinity

• Use top layer of e.g. ResNet-18 whose first 4 blocks take grayscale input
• Dense correspondence should have a sparse affinity matrix, but it’s hard to enforce this
  • they take a more relaxed approach and apply softmax over columns

$$A_{ij}=\frac{\exp \left(f_{1i}^{\top }{f}_{2j}\right)}{{\sum }_k\exp \left(f_{1k}^{\top }{f}_{2j}\right)},\forall i\in \left[1,N_1\right],j\in \left[1,N_2\right]$$

The transformation is carried out as $\widehat{c_2}=c_{1}A$, where $A\in {\mathcal{R}}^{N_1\times N_2}$, and $c_i$ has the same number of entries as $f_i$ and can be features of the reference frame or any associated label, e.g., color, segmentation mask or keypoint heatmap.

Tracing pixel locations We denote $l_j=\left(x_j,y_j\right),l\in {\mathcal{R}}^{2\times N}$ as the vectorized location map for an image/feature with $N$ pixels. Given a sparse affinity matrix, the location of an individual pixel can be traced from a reference frame to an adjacent target frame:

$$l_j^{12}=\sum _{k=1}^{N_1}{l}_k^{11}{A}_{kj},\forall j\in \left[1,N_2\right]$$

where $l_j^{mn}$ represents the coordinate in frame $m$ that transits to the $j^{th}$ pixel in frame $n$. Note that $l^{nn}$ (e.g., $l^{11}$ in (3)) usually represents a canonical grid as shown in Figure $3.$ 3.2 Region-level Localization In the target frame, region-level localization aims to localize a patch randomly selected from the reference frame by predicting a bounding box (denoted as “bbox”) on a region that shares matching parts with the selected patch. In other words, it is a differential region of interest (ROI) with learnable center and scale. We compute an $N_1\times N_2$ affinity $A_{pf}$ according to (2) between feature representations of the patch in the reference frame, and that of the whole target frame (see Figure $2(\mathrm{a}))$. Locating the center. To track the center position of the reference patch in the target frame, we first localize each individual pixel of the reference patch $p_1$ in the target frame $f_2$, according to (3). As we obtain the set $l^{21}$, with the same number of entries as $p_1$, that collects the coordinates of the most similar pixels in $f_2$, we can compute the average coordinate $C^{21}=\frac{1}{N_1}{\sum }_{i=1}^{N_1}{l}_i^{21}$ of all the points, as the estimated new position of the reference patch.

Interesting References

• Wang et al. (2019) Unsupervised deep tracking. CVPR
• Wang, Jabri and Efros (2019) Learning correspondence from the cycle-consistency of time. CVPR

---

VFS: Rethinking Self-supervised Correspondence Learning A Video Frame-level Similarity Perspective

Notes on Rethinking Self-supervised Correspondence Learning A Video Frame-level Similarity by Jiarui Xu and Xiaolong Wang.

• Paper: https://arxiv.org/pdf/2103.17263.pdf
• Code: https://github.com/xvjiarui/VFS/
• Paper Website: https://jerryxu.net/VFS/

Summary

Xu and Wang propose learning correspondence by exploiting the free temporal correspondence signal directly at the frame level on the supposition that convolutional layers should learn correspondences between objects (bounding boxes in the visual object tracking; OTB) and object parts (pixel level, i.e. the DAVIS video object segmentation task; VOS).

Note: The approach(es) taken by this paper are at their core quite simple⁵ so the results they get are to my mind the most interesting thing about this paper, especially the quirky but intuitive result they get which shows that colour augmentations affect pixel-level label propagation performance negatively but improve object-level tracking.

Main Results

They summarise their main results:

• Large frame gaps and multiple frame pairs improves correspondence
  • Fine-grained by ~3% (DAVIS)
  • Object-level by > 10% (OTB)
• Training with multiple frame pairs simultaneously improves performance even more.
  • I guess they mean constructing an affinity matrix with multiple positive pairs (see Pipeline)
• Colour augmentation is harmful for fine-grained correspondence (~3% DAVIS), but beneficial for object-level correspondence (~10% OTB; ‘future learns better object invariance’)
• Training without negative pairs improves both object-level and fine-grained performance - very surprising result!
• Deeper models exhibit better performance - SSL pretext task training for correspondence usually renders deeper nets redundant, meaning performance doesn’t improve going deeper e.g. ResNet-50 vs ResNet-18. But training with VFS’ pretext task using video frames does show improved (downstream) performance for deeper nets.

Approach

Their method is actually very simple, since it just straightforwardly applies contrastive methods from visual representation learning to video frames, leveraging the inherent augmentation of motion across time to learn using a similarity loss. In particular, they ‘unify’ methods with negative pairs, like SimCLR and MoCo, and ones without negative pairs, like BYOL and especially SimSiam. In doing this, they question (or even undermine) the utility of more elaborate object- or patch-tracking pretext task set-ups for learning correspondences, asking:

Do we really need to design self-supervised object (or patch) tracking task explicitly to learn correspondence? Can image-level similarity learning alone learn the correspondence?

They apply standard image augmentations on top of the selection of frames across time. This is especially interesting since they observe using colour augmentation is harmful for fine-grained correspondence (pixel-level; DAVIS VOS) but beneficial for object-level correspondence (OTB).

So basically, given two frames (or more pairs) sampled according to either strategy, possibly with additional augmentation they forward them to the predictor encoder, $\mathcal{P}$, and the target encoder, $\mathcal{T}$, do $l_2$ normalisation of the output representation⁶ and either…

use InfoNCE loss (from the CPC paper), like so

${\mathcal{L}}_{p_i,z_j,\mathcal{U}}=-\log \frac{\exp \left(p_i\cdot z_j/\tau \right)}{\exp \left(p_i\cdot z_j/\tau \right)+{\sum }_{k=1}^K\exp \left(p_i\cdot u_k/\tau \right)}$

or they don’t use negative pairs (SimSiam, BYOL) and minimise the loss

${\mathcal{L}}_{p_i,z_j}={\Vert p_i-z_j\Vert }_2^2=2-2\cdot p_i\cdot z_j$

Implementation

It’s nice because they unify the with negative pairs and without negative pairs approaches but using very consistent implementation, which they take directly from Xinlei Chen and Kaiming He (along with those guys’ colleagues) so they use

• With Negative Pairs: Improved baselines with momentum contrastive learning - this is the extension paper to MoCo, let’s say MoCo v2
• Without Negative Pairs: Exploring simple siamese representation learning - SimSiam

(Pre-)Training (emphasis mine):

We adopt the Kinetics [41] dataset for self-supervised training. It consists of ∼240k training videos. The batch size is 256. The learning rate is initialized to 0.05, and decays in the cosine schedule [12, 49, 13]. We use SGD optimizer with momentum 0.9 and weight decay 0.0001. We found that training for 100 epochs is sufficient for ResNet-18 models, and ResNet-50 models need 500 epochs to converge (roughly the same number of iterations as 100 epochs training [14] on ImageNet).

Pipeline

{:refdef: style=“text-align: center;“} {: refdef}

The affinity matrix is the pairwise feature similarity between predictor features and target features.

The dash rectangle areas indicate the with negative pairs case. [Negative pairs are one of the two research streams they pursue to train their model. Remember that you can use stop-grad like SimSiam or a momentum encoder like BYOL.]

The features of negative samples are stored in the negative bank [like MoCo, which uses a “queue” of negative samples in conjunction with a momentum encoder] and concatenate with target features.

The encoder is trained to maximize the affinity of positive pairs and minimize the affinity of negative ones.

Video Frame Sampling

Continuous sampling: They either sample over constant intervals, $\delta$, - from a video of length $L$ to get frames $I_i\in [1,L]$ or…
Distant sampling: Split the length-$L$ video into $n$ disjoint segments and take a random frame from each segment randomly, according to $I_i=\frac{L}{n}(i-1)+\mathrm{unif}\left(0,\frac{L}{n}\right)$

{:refdef: style=“text-align: center;“} {: refdef}

Sidenote: They comment that continuous (consistent) sampling is more common when using 3D Convolution as used in Learning spatiotemporal features with 3d convolutional networks or Quo Vadis, Action Recognition? A New Model and the Kinetics Dataset.

Augmentations

• Spatial: Random cropping and flipping
• Colour augmentation: grayscale and colour jitter - Affects OTB vs VOS downstream performance, see Main Results

Results

First a few details:

• Fine-grained correspondence:
  • fine-grained similarity is measured on the ${\text{res}}_4$ feature map, with its stride reduced to 1 during inference
  • Recurrent inference strategy used: First ground-truth frame and latest 20 predicted frames are propagated to the current frame
  • DAVIS for VOS, pose-tracking done in JHMDB and human-part tracking in VIP
• Object-level correspondence:
  • evaluate object-level correspondence with visual object tracking in the OTB-100 [78] dataset
  • they use SiamFC tracking with the representation from their trained res${}_5$ block
  • Given the pretrained ResNet, the strides in res${}_4$ and res${}_5$ are removed and dilations of 2 and 4 are added to these block respectively - makes the res${}_5$ block output compatible with SiamFC but does not affect the pretrained weights
  • Most of their analysis is on a frozen ResNet then comparisons to SotA is with fine-tuning (end of paper)

Results: Downstream Performance on DAVIS and OTB

{:refdef: style=“text-align: center;“} {: refdef}

• Colour augmentation helps object-level and harms pixel-level correspondence
• Spatial augmentations help both
• Temporal sampling further apart (with a constant step) is better, and sampling according to the distant sampling (uniform in a segment) approach is best (with 2 disjoint segments, i.e. 2 frames)
• Using more frames from a single video is better
• Using negative pairs worsens performance

What is the reason causing this performance drop when training with negatives?

Our hypothesis is that training with negative pairs may sacrifice the performance on modeling intra-instance invariance for learning better features for cross instance discrimination.

To prove this hypothesis, we perform linear classification on top of the frozen features on the ImageNet-1k dataset [18] and report the results on the right column of Table 5.

We observe that the model trained with negatives indeed leads to better semantic classification with around 2% improvement, which supports our hypothesis.

• Different blocks of the res$\_4$ and res$\_5$ layers specialise in a sense
  • res${}_4$ is better at fine-grained correspondence tasks
  • res${}_5$ focuses on object-level

They evaluate J&F mean scores on DAVIS at different epochs using the features of different blocks from the res${}_4$ and res${}_5$ layers as a nice ablation study

{:refdef: style=“text-align: center;“} {: refdef}

Comparison to SotA

VFS outperforms all SotA benchmarks on object-level tasks with ResNet-18 or ResNet-50 backbones.

{:refdef: style=“text-align: center;“} {: refdef}

For the fine-grained correspondence, they surpass all SotA benchmarks except Contrastive Random Walk (CRW; or “Videowalk”) for ResNet-18, and for ResNet-50 they are always best, although they don’t compare against CRW because they couldn’t get the architecture to work for the deeper backbone.

{:refdef: style=“text-align: center;“} {: refdef}

Additional Notes

Some additional small points.

SyncBN

They use Synchronised Batch Normalisation, which is batch norm used for multi-GPU training wherein the batch norm statistics (mean and standard deviation) are calculated across the whole minibatch, i.e. across all the GPUs used for training.

This is different from what would happen otherwise, where the statistics would only by computed within each GPU. (Remember that when you set the batch size in PyTorch when using multiple GPUs for training, you in practice send a minibatch of size $\text{batch size}/N_{\text{GPUs}}$ to each GPU.)

You can use SyncBatchNorm with torch.nn.SyncBatchNorm which applies batch norm but ensures [t]he mean and standard-deviation are calculated per-dimension over all mini-batches of the same process groups.

See also the PyTorch SyncBatchNorm source code and Zhang et al. Context Encoding for Semantic Segmentation, which made use of it for the first time.

Authors’ Conclusions

1. Tracking-based pretext tasks are not necessary for self-supervised correspondence learning

Is designing a tracking-based pretext task a necessity for self-supervised correspondence learning? It might not be necessary. While tracking-based pretext tasks still have potentials, it is limited by small backbone models and is now surpassed by our simple frame-level similarity learning. To make the tracking-based pretext tasks useful, we need to first make its learning scalable and generalizable in model size and network architectures.

2. Colour augmentation improves object tracking and worsens pixel-level tracking

color augmentation is beneficial for correspondence in object-level but jeopardizes the fine- grained correspondence. While color augmentation brings object appearance invariance, it also confuses the lower- layer convolution features

3. Sample multiple frames and sample with a large gap

The large temporal gap provides more aggressive temporal transform, which boosts correspondence significantly. Comparing multiple pairs of frame further improves the results

4. Negative pairs decrease performance, let alone being not necessary for contrastive learning when learning via self-supervised correspondence

We observe inferior performance when training with negative samples, specifically for object-level correspondence. We also shed light on the reason why without negative pairs is more helpful, which has not been studied before

Implementation

Watch out for the strange structure of the VFS repository, that uses MMCV (a tool I haven’t personally used at the time of writing, but which looks useful for modularising tests and model builds) to do the model builds.

The models reside in VFS/mmaction/models but are built with (what are in the end calls to) the build function in builder.py in that directory.

---

Footnotes

1. 0.3% accuracy is reported when removing the momentum encoder; see Table 5 of the BYOL paper. In BYOL’s arXiv v3 update, it reports 66.9% accuracy with 300-epoch pre-training when removing the momentum encoder and increasing the predictor’s learning rate by 10×. Our work was done concurrently with this arXiv update. Our work studies this topic from different perspectives, with better results achieved. ↩

2. A stop-gradient is required for a momentum-encoder because the momentum-encoder’s weights are updated as an exponential moving average of the current and previous iterations’ encoder weights _from the other branch of the networks, which gradients backpropagate through. So obviously this update is done independently of any gradients that flow back through the momentum-encoder branch of the network / the set-up. That said, as the authors (of SimSIam) say even though MoCo [17] and BYOL [15] do not directly share the weights between the two branches, … the momentum encoder should converge to the same status as the trainable encoder [so] these models [can be viewed] as Siamese networks with “indirect” weight-sharing. 🤭 ↩

3. Remember, we’re talking about an output representation from a vision encoder, so vector elements are output channels. ↩

4. Using a bigger ResNet encoder, they get the benchmark accuracy up to 79.6% ↩

5. …and borrow heavily from MoCo and SimSiam (along with related papers) for the method and implementation, but they apply this using video… ↩

6. Remember that it is very important to norm the output representations of networks when using contrastive losses, since otherwise you are allowing the different magnitudes of the representation vectors (and their elements) to count in facilitating discrimination between positive and negative pairs. (In the case where no negative pairs are used, I suppose there’s some implicit mechanism that renders this a problem for analogous reasons.) ↩