Momentum Contrast for Unsupervised Visual Representation Learning

Title: Momentum Contrast for Unsupervised Visual Representation Learning
Authors: Kaiming He, Haoqi Fan, Yuxin Wu, Saining Xie, Ross Girshick
Published: 13th November 2019 (Wednesday) @ 18:53:26
Link: http://arxiv.org/abs/1911.05722v3

Abstract

We present Momentum Contrast (MoCo) for unsupervised visual representation learning. From a perspective on contrastive learning as dictionary look-up, we build a dynamic dictionary with a queue and a moving-averaged encoder. This enables building a large and consistent dictionary on-the-fly that facilitates contrastive unsupervised learning. MoCo provides competitive results under the common linear protocol on ImageNet classification. More importantly, the representations learned by MoCo transfer well to downstream tasks. MoCo can outperform its supervised pre-training counterpart in 7 detection/segmentation tasks on PASCAL VOC, COCO, and other datasets, sometimes surpassing it by large margins. This suggests that the gap between unsupervised and supervised representation learning has been largely closed in many vision tasks.

Notes on MoCo: Momentum Contrast for Unsupervised Visual Representation Learning by Kaiming He and colleagues.

Paper: https://arxiv.org/pdf/1911.05722.pdf
Code: https://github.com/facebookresearch/moco

Abstract broken up with some added emphasis:

We present Momentum Contrast (MoCo) for unsupervised visual representation learning. From a perspective on contrastive learning [29] as dictionary look-up, we build a dynamic dictionary with a queue and a moving-averaged encoder. This enables building a large and consistent dictionary on-the-fly that facilitates contrastive unsupervised learning.

MoCo provides competitive results under the common linear protocol on ImageNet classification.

More importantly, the representations learned by MoCo transfer well to downstream tasks. MoCo can outperform its supervised pre-training counterpart in 7 detection/segmentation tasks on PASCAL VOC, COCO, and other datasets, sometimes surpassing it by large margins.

This suggests that the gap between unsupervised and supervised representation learning has been largely closed in many vision tasks.

Introduction

Authors state the continuous signal space of computer vision makes it less amenable to self-supervised techniques as compared to NLP, whose samples are constituted of token form a finite signal space, concretely of the vocabulary size:

The reason may stem from differences in their respective signal spaces. Language tasks have discrete signal spaces (words, sub-word units, etc.) for building tokenized dictionaries, on which unsupervised learning can be based. Computer vision, in contrast, further concerns dictionary building [54, 9, 5], as the raw signal is in a continuous, high-dimensional space and is not structured for human communication (e.g., unlike words)

They frame contrastive learning in terms of dictionary look-up against dynamic dictionaries:

[Contrastive learning] can be thought of as building dynamic dictionaries. The “keys” (tokens) in the dictionary are sampled from data (e.g., images or patches) and are represented by an encoder network. Unsupervised learning trains encoders to perform dictionary look-up: an encoded “query” should be similar to its matching key and dissimilar to others. Learning is formulated as minimizing a contrastive loss¹

They target having dictionaries (for looking up query image views against) that are:

Large
Consistent as they evolve (see [#inconsistency-of-encoded-representations])

The momentum contrast dictionary is a queue of data samples, where the latest minibatch is enqueued and the oldest is dequeued.
This decouples the dictionary size from the batch size.
The key encoder for encoding the dictionary entries (samples) is a momentum-based moving average of the query encoder, proposed to maintain consistency of the keys against which new samples are queried in the contrastive loss.

Et voilà, MoCo 😉

Interestingly, it is appropriate to think of MoCo as a way of building dynamic dictionaries for any kind of contrastive learning, so you can swap out different pretext tasks:

MoCo is a mechanism for building dynamic dictionaries for contrastive learning, and can be used with various pretext tasks. In this paper, we follow a simple instance discrimination task [61, 63, 2]: a query matches a key if they are encoded views (e.g., different crops) of the same image.

As we know with self-supervised learning, we have pretext tasks + loss functions:

self-supervised learning methods generally involve two aspects: pretext tasks and loss functions.

The term “pretext” implies that the task being solved is not of genuine interest, but is solved only for the true purpose of learning a good data representation.

Loss functions can often be investigated independently of pretext tasks. MoCo focuses on the loss function aspect.

Contrastive Learning as Dictionary Look-up

The authors use the InfoNCE loss:

$L_{q} = - lo g \frac{e x p ( q \cdot k _{+} / τ )}{\sum _{i = 0}^{K} e x p ( q \cdot k _{i} / τ )}$

As can be seen, this is a simple negative log-softmax where the correct class is the positive key, $k_{+}$ , and the denominator indexes over all keys in the dictionary.

Additionally, a temperature hyperparameter, $τ$ , is used for tuning. Using a high temperature makes the probability distribution more diffuse across classes (i.e. ‘softer’) and means we obtain predictions with higher uncertainty. Conversely, using a low temperature makes the probability distribution ‘harder’, reducing uncertainty of the predictions; setting $τ = 1$ of course reduces this to the regular (negative log-)softmax. (Temperature as a softmax hyperparameter is explained here and demonstrated practically in this post.)

Keep in mind, contrastive losses can be based on margins (e.g. based on hinge loss for positive and negative samples) or other variants of NCE losses.

Key Ideas: Momentum and the Queue of Keys

I added numbers (1) and (2) to the extract below to emphasise MoCo’s two main conributions:

Use momentum (an exponential moving average) to update the key encoder on the basis of the current iteration’s query encoder and (a weighted combination of) past iterations’ query parameters.
Use a queue to keep the negative samples for a additional, manageable memory overhead that enables use of a larger range of negative samples.

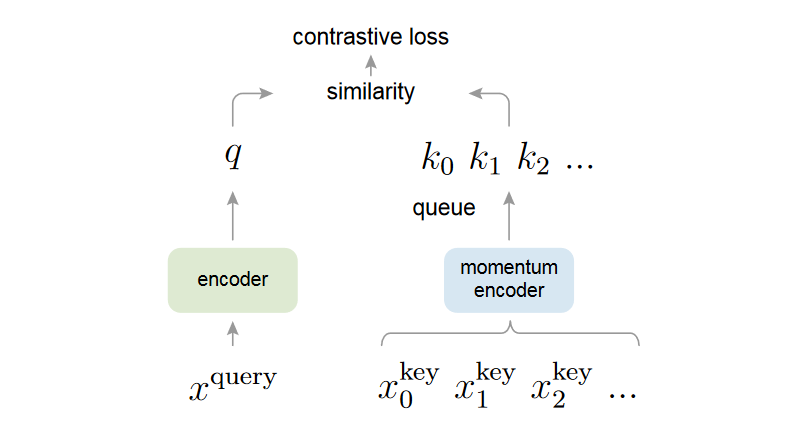
Figure 1. Momentum Contrast (MoCo) trains a visual representation encoder by matching an encoded query $q$ to a dictionary of encoded keys using a contrastive loss. The dictionary keys $k 0, k 1, k 2, \dots$ are defined on-the-fly by a set of data samples.

The dictionary is built as a queue, with the current mini-batch enqueued and the oldest mini-batch dequeued, decoupling it from the mini-batch size.

The keys are encoded by a slowly progressing encoder, driven by a momentum update with the query encoder. This method enables a large and consistent dictionary for learning visual representations.

Algorithm

The above is the algorithm for MoCo.

We initialise the parameters of the key encoder as the same randomly initialised parameters as the query encoder.

Then for each minibatch:

Create two randomly augmented versions of the input images (in current minibatch)
Run the forward pass of the query image(s) through the query encoder and key image(s) through the key encoder
Calculate positive logit(s)² which come from the matrix multiplication of the query and key image(s)
- NOTE: If the batch size were 1, there would be only 1 positive logit corresponding to the positive sample
Calculate negative logits which come from the matrix multiplication of the query and queue images
Concatenate the positive and negative logits
Compute the contrastive InfoNCE loss as the softmax shown before
- in the algorithm, they use the label vector as an $N$ -dimensional vector of zeros since they put the positive logit in the first position via cat[l_pos, l_neg], dim=1)
Backpropagate gradients
Update the query encoder parameters only via the optimiser (using the computed gradients)
Update the key encoder via a momentum (exponential moving average) update: $θ_{key} = m \cdot θ_{key} + (m - 1) \cdot θ_{query}$ where they use $m = 0.999$ (see Implementation)
- This places most of the weight for the update on parameter values from previous iterations, but still allows more recent iterations to contribute significantly over the course of e.g. an epoch

Shuffling Batch Norm: Batch Normalisation Leaking Information

The authors shuffle batch normalisation in order to prevent the model from using BN layers to exploit information across batches to decrease the loss on the pretext task without improving the quality (downstream performance) of the learnt encoder.

This happens because performing batch norm leaks mean and variance statistics across batches, allowing the model to set the $α$ and $β$ learn parameters of the BN layer to better fit the training data better in a trivial fashion.

Shuffling BN. Our encoders $f_{q}$ and $f_{k}$ both have Batch Normalization (BN) [37] as in the standard ResNet [33]. In experiments, we found that using BN prevents the model from learning good representations, as similarly reported in [35] (which avoids using BN). The model appears to “cheat” the pretext task and easily finds a low-loss solution. This is possibly because the intra-batch communication among samples (caused by BN) leaks information.

Specifically, the condition they satisfy is:

[ensuring] the batch statistics used to compute a query and its positive key come from two different [data] subsets. This effectively tackles the cheating issue and allows training to benefit from BN.

The way they do this is fiddly:

We resolve this problem by shuffling BN. We train with multiple GPUs and perform BN on the samples independently for each GPU (as done in common practice). For the key encoder $f_{k}$ , we shuffle the sample order in the current mini-batch before distributing it among GPUs (and shuffle back after encoding); the sample order of the mini-batch for the query encoder $f_{q}$ is not altered.

The SSL set-up that uses a memory bank (one of the two previous self-supervised set-ups they compare against) doesn’t suffer from this information leakage problem since the positive keys are from different, previous batches.

What is the Dictionary Queue

MoCo uses a queue to represent the dictionary of keys that make up negative samples to contrast the positive augmented sample against; when putting the query through the contrastive loss.

How does the dictionary queue work? Implementation

The dictionary is implemented as a queue.

Specifically, in the PyTorch implementation, in the MoCo class __init__ body, they:

register a buffer (see What is a buffer in PyTorch) of dimension (feature dimension $\times$ queue size), randomly initialised to use as a queue
register another buffer to use as a pointer for the queue

def __init__(self, base_encoder, dim=128, K=65536, m=0.999, T=0.07, mlp=False):
    '''
    dim: feature dimension (default: 128)
    K: queue size; number of negative keys (default: 65536)
    '''
 
    # ...
 
    # create the queue
    self.register_buffer("queue", torch.randn(dim, K))
    self.queue = nn.functional.normalize(self.queue, dim=0)
 
    self.register_buffer("queue_ptr", torch.zeros(1, dtype=torch.long))

Then, they have a method (decorated with @torch.no_grad()) that they call at the end of every iteration, i.e. at the end of the forward pass.

They pass k the encoded keys to the function to “enqueue” them, whilst “dequeuing” the oldest ones, which they track by moving the queue pointer along by the batch size each time: ptr = (ptr + batch_size) % self.K # move pointer. As we can see, there’s no actual enqueuing and dequeuing happening, and instead by using a pointer they just directly replace the oldest (encoded) keys with the new batch of (encoded) keys.

@torch.no_grad()
def _dequeue_and_enqueue(self, keys):
    # gather keys before updating queue
    keys = concat_all_gather(keys)
 
    batch_size = keys.shape[0]
 
    ptr = int(self.queue_ptr)
    assert self.K % batch_size == 0  # for simplicity
 
    # replace the keys at ptr (dequeue and enqueue)
    self.queue[:, ptr:ptr + batch_size] = keys.T
    ptr = (ptr + batch_size) % self.K  # move pointer
 
    self.queue_ptr[0] = ptr

So basically, as is evident from the above, the added memory overhead is an additional Tensor of size dim by K. Given that When PyTorch is initialized its default floating point dtype is torch.float32 (mentioned at the torch.set_default_dtype) docs), which is a 32-bit floating point, we have a memory overhead of:

32 bits $\times$ dim $\times$ K
For default values of $128 = 2^{7}$ and $65536 = 2^{16}$ we have:
- $32 \times 128 \times 65536 = 2^{5} \cdot 2^{7} \cdot 2^{16} = 2^{28} = 268435456$ bits
- $= 2^{25} = 33554432$ bytes
- or $\approx 33.5$ MB

What is a buffer in PyTorch

A Module buffer is a Tensor attribute of a Module that is not a model Parameter

See the register_buffer method in the docs for Module:

Adds a buffer to the module.

This is typically used to register a buffer that should not to be considered a model parameter. For example, BatchNorm’s running_mean is not a parameter, but is part of the module’s state. Buffers, by default, are persistent and will be saved alongside parameters. This behavior can be changed by setting persistent to False. The only difference between a persistent buffer and a non-persistent buffer is that the latter will not be a part of this module’s state_dict.

Buffers can be accessed as attributes using given names.

Details

Remember to always take the (e.g. L2) norm of the feature representation of an image returned by the encoder to put it into a contrastive loss.

Comparison to Previous Self-Supervised Approaches

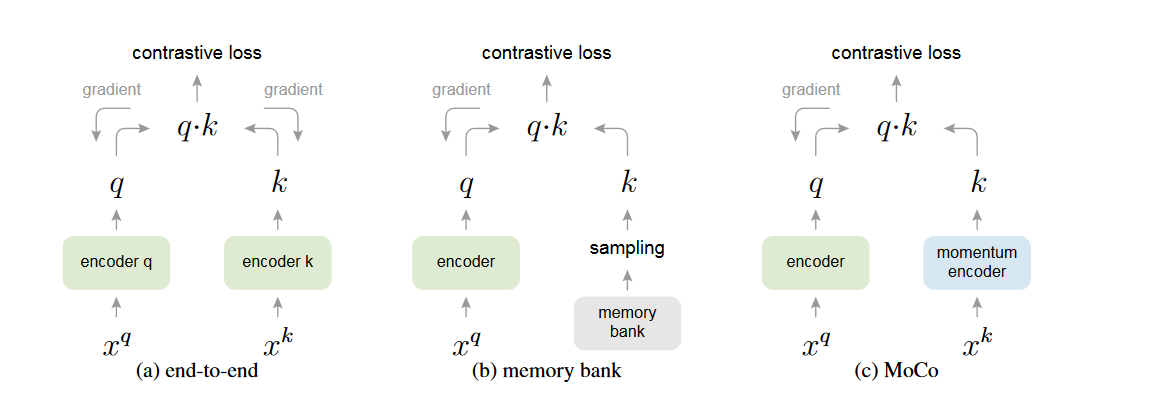
In comparison to previous approaches, you

Don’t have this issue of inconsistent key representations during training when you do the update with gradients
- this corresponds to the end-to-end model (a) pictured above
Don’t require a heavy memory bank
- this is (b) as devised in Unsupervised Feature Learning via Non-Parametric Instance Discrimination by Zhirong Wu and colleagues from 2018

Inconsistency of encoded representations

Why Was MoCo Proposed? The following sets the ground for part of the reason why MoCo was necessary given the context of SimCLR being the prevailing / landmark self-supervised visual representation learning.

It is taken from Understanding Contrastive Learning and MoCo: What is important in contrastive learning and how it can help by Shuchen Du:

Inconsistency of encoded representations

In SimCLR, we have only one encoder through which a mini-batch is passed then positive and negative pairs are constructed for training. In this way, positive and negative pairs are consistent, which means they are generated from an encoder with the same parameters. On the other hand, the parameters of the encoder are not changed during the generation of all pair data in a mini-batch. That is important because the parameters of the encoder are updated per mini-batch, thus for the same input image, the generated representations will be different from different mini-batches. This phenomenon is called inconsistent representation generation. Since the encoder is updated every mini-batch, the generated representations in current mini-batch will be getting ‘old’ compared to those generated in the future mini-batches. Therefore, it is not optimal to mix representations from different mini-batches and use them together during training. It is also the reason why SimCLR uses large batch sizes.

Before MoCo is proposed, people tend to use a memory bank to keep a large amount of inconsistent representations to meet the demand of large amount of negative pair constructions. However, the performance is not good due to the sub-optimal inconsistent representations. Therefore, MoCo is proposed to convert the representations encoded from different mini-batches from inconsistency to consistency.

As the authors say themselves in the text (see Introduction):

…while the keys in the dictionary should be represented by the same or similar encoder so that their comparisons to the query are consistent.

Implementation

For concreteness, here is the implementation of the MoCo class as a torch.nn.Module.

Up top, we can see that they use default values of

Very large momentum value, $m = 0.999$ , so that the key encoder network’s parameters are basically constant, instead of updated each minibatch like in previous work (e.g. SimCLR) with a small contribution from the current iteration’s parameter values.
- Of course over the course of an epoch, this relative weighting in the EMA will lead to significant contributions from up-to-date iterations
Temperature of 0.07 which is a common choice
Key queue size of $65, 536 = 2^{16}$ (probably a power of two to fit nicely into memory on the even number of GPUs)

In the initialisation method arguments, we have the defaults:

K=65536, m=0.999, T=0.07

import torch
import torch.nn as nn
 
 
class MoCo(nn.Module):
    """
    Build a MoCo model with: a query encoder, a key encoder, and a queue
    https://arxiv.org/abs/1911.05722
    """
    def __init__(self, base_encoder, dim=128, K=65536, m=0.999, T=0.07, mlp=False):
        """
        dim: feature dimension (default: 128)
        K: queue size; number of negative keys (default: 65536)
        m: moco momentum of updating key encoder (default: 0.999)
        T: softmax temperature (default: 0.07)
        """
        super(MoCo, self).__init__()
 
        self.K = K
        self.m = m
        self.T = T
 
        # create the encoders
        # num_classes is the output fc dimension
        self.encoder_q = base_encoder(num_classes=dim)
        self.encoder_k = base_encoder(num_classes=dim)
 
        if mlp:  # hack: brute-force replacement
            dim_mlp = self.encoder_q.fc.weight.shape[1]
            self.encoder_q.fc = nn.Sequential(nn.Linear(dim_mlp, dim_mlp), 
                                              nn.ReLU(), 
                                              self.encoder_q.fc)
            self.encoder_k.fc = nn.Sequential(nn.Linear(dim_mlp, dim_mlp), 
                                              nn.ReLU(), 
                                              self.encoder_k.fc)
 
        for param_q, param_k in zip(self.encoder_q.parameters(), self.encoder_k.parameters()):
            param_k.data.copy_(param_q.data)  # initialize
            param_k.requires_grad = False  # not update by gradient
 
        # create the queue
        self.register_buffer("queue", torch.randn(dim, K))
        self.queue = nn.functional.normalize(self.queue, dim=0)
 
        self.register_buffer("queue_ptr", torch.zeros(1, dtype=torch.long))
 
    @torch.no_grad()
    def _momentum_update_key_encoder(self):
        """
        Momentum update of the key encoder
        """
        for param_q, param_k in zip(self.encoder_q.parameters(), self.encoder_k.parameters()):
            param_k.data = param_k.data * self.m + param_q.data * (1. - self.m)
 
    @torch.no_grad()
    def _dequeue_and_enqueue(self, keys):
        # gather keys before updating queue
        keys = concat_all_gather(keys)
 
        batch_size = keys.shape[0]
 
        ptr = int(self.queue_ptr)
        assert self.K % batch_size == 0  # for simplicity
 
        # replace the keys at ptr (dequeue and enqueue)
        self.queue[:, ptr:ptr + batch_size] = keys.T
        ptr = (ptr + batch_size) % self.K  # move pointer
 
        self.queue_ptr[0] = ptr
 
    @torch.no_grad()
    def _batch_shuffle_ddp(self, x):
        """
        Batch shuffle, for making use of BatchNorm.
        *** Only support DistributedDataParallel (DDP) model. ***
        """
        # gather from all gpus
        batch_size_this = x.shape[0]
        x_gather = concat_all_gather(x)
        batch_size_all = x_gather.shape[0]
 
        num_gpus = batch_size_all // batch_size_this
 
        # random shuffle index
        idx_shuffle = torch.randperm(batch_size_all).cuda()
 
        # broadcast to all gpus
        torch.distributed.broadcast(idx_shuffle, src=0)
 
        # index for restoring
        idx_unshuffle = torch.argsort(idx_shuffle)
 
        # shuffled index for this gpu
        gpu_idx = torch.distributed.get_rank()
        idx_this = idx_shuffle.view(num_gpus, -1)[gpu_idx]
 
        return x_gather[idx_this], idx_unshuffle
 
    @torch.no_grad()
    def _batch_unshuffle_ddp(self, x, idx_unshuffle):
        """
        Undo batch shuffle.
        *** Only support DistributedDataParallel (DDP) model. ***
        """
        # gather from all gpus
        batch_size_this = x.shape[0]
        x_gather = concat_all_gather(x)
        batch_size_all = x_gather.shape[0]
 
        num_gpus = batch_size_all // batch_size_this
 
        # restored index for this gpu
        gpu_idx = torch.distributed.get_rank()
        idx_this = idx_unshuffle.view(num_gpus, -1)[gpu_idx]
 
        return x_gather[idx_this]
 
    def forward(self, im_q, im_k):
        """
        Input:
            im_q: a batch of query images
            im_k: a batch of key images
        Output:
            logits, targets
        """
 
        # compute query features
        q = self.encoder_q(im_q)  # queries: NxC
        q = nn.functional.normalize(q, dim=1)
 
        # compute key features
        with torch.no_grad():  # no gradient to keys
            self._momentum_update_key_encoder()  # update the key encoder
 
            # shuffle for making use of BN
            im_k, idx_unshuffle = self._batch_shuffle_ddp(im_k)
 
            k = self.encoder_k(im_k)  # keys: NxC
            k = nn.functional.normalize(k, dim=1)
 
            # undo shuffle
            k = self._batch_unshuffle_ddp(k, idx_unshuffle)
 
        # compute logits
        # Einstein sum is more intuitive
        # positive logits: Nx1
        l_pos = torch.einsum('nc,nc->n', [q, k]).unsqueeze(-1)
        # negative logits: NxK
        l_neg = torch.einsum('nc,ck->nk', [q, self.queue.clone().detach()])
 
        # logits: Nx(1+K)
        logits = torch.cat([l_pos, l_neg], dim=1)
 
        # apply temperature
        logits /= self.T
 
        # labels: positive key indicators
        labels = torch.zeros(logits.shape[0], dtype=torch.long).cuda()
 
        # dequeue and enqueue
        self._dequeue_and_enqueue(k)
 
        return logits, labels
 
 
# utils
@torch.no_grad()
def concat_all_gather(tensor):
    """
    Performs all_gather operation on the provided tensors.
    *** Warning ***: torch.distributed.all_gather has no gradient.
    """
    tensors_gather = [torch.ones_like(tensor)
        for _ in range(torch.distributed.get_world_size())]
    torch.distributed.all_gather(tensors_gather, tensor, async_op=False)
 
    output = torch.cat(tensors_gather, dim=0)
    return output

Raia Hadsell, Sumit Chopra, and Yann LeCun. Dimensionality reduction by learning an invariant mapping. In CVPR, 2006 ↩
“Logits” in the deep learning sense actually doesn’t correspond to logits in the actual, statistics sense where it means the log of the odds. Instead logits in the context of neural networks means the raw, unnormalised network outputs (e.g. before the softmax layer). ↩

🪴 Anil's Garden

Explorer

Momentum Contrast for Unsupervised Visual Representation Learning

Introduction

Contrastive Learning as Dictionary Look-up

Key Ideas: Momentum and the Queue of Keys

Algorithm

Shuffling Batch Norm: Batch Normalisation Leaking Information

What is the Dictionary Queue

How does the dictionary queue work? Implementation

What is a buffer in PyTorch

Details

Comparison to Previous Self-Supervised Approaches

Inconsistency of encoded representations

Implementation

Graph View

Table of Contents

Backlinks

🪴 Anil's Garden

Explorer

Momentum Contrast for Unsupervised Visual Representation Learning

Introduction

Contrastive Learning as Dictionary Look-up

Key Ideas: Momentum and the Queue of Keys

Algorithm

Shuffling Batch Norm: Batch Normalisation Leaking Information

What is the Dictionary Queue

How does the dictionary queue work? Implementation

What is a buffer in PyTorch

Details

Comparison to Previous Self-Supervised Approaches

Inconsistency of encoded representations

Implementation

Footnotes

Graph View

Table of Contents

Backlinks