Dynamic time warping - Wikipedia

From Wikipedia, the free encyclopedia

An algorithm for measuring similarity between two temporal sequences, which may vary in speed

Dynamic time warping between two piecewise linear functions. The dotted line illustrates the time-warp relation. Notice that several points in the lower function are mapped to one point in the upper function, and vice versa.

Two repetitions of a walking sequence recorded using a motion-capture system. While there are differences in walking speed between repetitions, the spatial paths of limbs remain highly similar.¹

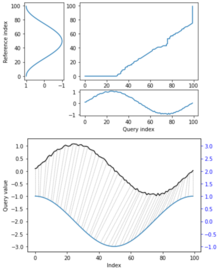
DTW between a sinusoid and a noisy and shifted version of it.

In time series analysis, dynamic time warping (DTW) is an algorithm for measuring similarity between two temporal sequences, which may vary in speed. For instance, similarities in walking could be detected using DTW, even if one person was walking faster than the other, or if there were accelerations and decelerations during the course of an observation. DTW has been applied to temporal sequences of video, audio, and graphics data — indeed, any data that can be turned into a one-dimensional sequence can be analyzed with DTW. A well-known application has been automatic speech recognition, to cope with different speaking speeds. Other applications include speaker recognition and online signature recognition. It can also be used in partial shape matching applications.

In general, DTW is a method that calculates an optimal match between two given sequences (e.g. time series) with certain restriction and rules:

We can plot each match between the sequences $1:M$ and $1:N$ as a path in a $M\times N$ matrix from $(1,1)$ to $(M,N)$ , such that each step is one of $(0,1),(1,0),(1,1)$ . In this formulation, we see that the number of possible matches is the Delannoy number.

The optimal match is denoted by the match that satisfies all the restrictions and the rules and that has the minimal cost, where the cost is computed as the sum of absolute differences, for each matched pair of indices, between their values.

The sequences are “warped” non-linearly in the time dimension to determine a measure of their similarity independent of certain non-linear variations in the time dimension. This sequence alignment method is often used in time series classification. Although DTW measures a distance-like quantity between two given sequences, it doesn’t guarantee the triangle inequality to hold.

In addition to a similarity measure between the two sequences (a so called “warping path” is produced), by warping according to this path the two signals may be aligned in time. The signal with an original set of points X(original), Y(original) is transformed to X(warped), Y(warped). This finds applications in genetic sequence and audio synchronisation. In a related technique sequences of varying speed may be averaged using this technique see the average sequence section.

This is conceptually very similar to the Needleman–Wunsch algorithm.

This example illustrates the implementation of the dynamic time warping algorithm when the two sequences s and t are strings of discrete symbols. For two symbols x and y, d(x, y) is a distance between the symbols, e.g. d(x, y) = $|x-y|$ .

int DTWDistance(s: array [1..n], t: array [1..m]) {
    DTW := array [0..n, 0..m]
    
    for i := 0 to n
        for j := 0 to m
            DTW[i, j] := infinity
    DTW[0, 0] := 0
    
    for i := 1 to n
        for j := 1 to m
            cost := d(s[i], t[j])
            DTW[i, j] := cost + minimum(DTW[i-1, j  ],    // insertion
                                        DTW[i  , j-1],    // deletion
                                        DTW[i-1, j-1])    // match
    
    return DTW[n, m]
}

where DTW[i, j] is the distance between s[1:i] and t[1:j] with the best alignment.

We sometimes want to add a locality constraint. That is, we require that if s[i] is matched with t[j], then $|i-j|$ is no larger than w, a window parameter.

We can easily modify the above algorithm to add a locality constraint (differences marked). However, the above given modification works only if $|n-m|$ is no larger than w, i.e. the end point is within the window length from diagonal. In order to make the algorithm work, the window parameter w must be adapted so that $|n-m|\le w$ (see the line marked with (*) in the code).

int DTWDistance(s: array [1..n], t: array [1..m], w: int) {
    DTW := array [0..n, 0..m]

    w := max(w, abs(n-m)) // adapt window size (*)

    for i := 0 to n
        for j:= 0 to m
            DTW[i, j] := infinity
    DTW[0, 0] := 0
    for i := 1 to n
        for j := max(1, i-w) to min(m, i+w)
            DTW[i, j] := 0

    for i := 1 to n
        for j := max(1, i-w) to min(m, i+w)
            cost := d(s[i], t[j])
            DTW[i, j] := cost + minimum(DTW[i-1, j  ],    // insertion
                                        DTW[i  , j-1],    // deletion
                                        DTW[i-1, j-1])    // match
    return DTW[n, m]
}

The DTW algorithm produces a discrete matching between existing elements of one series to another. In other words, it does not allow time-scaling of segments within the sequence. Other methods allow continuous warping. For example, Correlation Optimized Warping (COW) divides the sequence into uniform segments that are scaled in time using linear interpolation, to produce the best matching warping. The segment scaling causes potential creation of new elements, by time-scaling segments either down or up, and thus produces a more sensitive warping than DTW’s discrete matching of raw elements.

The time complexity of the DTW algorithm is $O(NM)$ , where $N$ and $M$ are the lengths of the two input sequences. The 50 years old quadratic time bound was broken in 2016: an algorithm due to Gold and Sharir enables computing DTW in $O(N^2/\log \log N)$ time and space for two input sequences of length $N$ .² This algorithm can also be adapted to sequences of different lengths. Despite this improvement, it was shown that a strongly subquadratic running time of the form $O(N^{2-ϵ})$ for some $ϵ>0$ cannot exist unless the Strong exponential time hypothesis fails.³⁴

While the dynamic programming algorithm for DTW requires $O(NM)$ space in a naive implementation, the space consumption can be reduced to $O(\min (N,M))$ using Hirschberg’s algorithm.

Fast techniques for computing DTW include PrunedDTW,⁵ SparseDTW,⁶ FastDTW,⁷ and the MultiscaleDTW.⁸⁹

A common task, retrieval of similar time series, can be accelerated by using lower bounds such as LB_Keogh,¹⁰ LB_Improved,¹¹ or LB_Petitjean.¹² However, the Early Abandon and Pruned DTW algorithm reduces the degree of acceleration that lower bounding provides and sometimes renders it ineffective.

In a survey, Wang et al. reported slightly better results with the LB_Improved lower bound than the LB_Keogh bound, and found that other techniques were inefficient.¹³ Subsequent to this survey, the LB_Enhanced bound was developed that is always tighter than LB_Keogh while also being more efficient to compute.¹⁴ LB_Petitjean is the tightest known lower bound that can be computed in linear time.¹²

Averaging for dynamic time warping is the problem of finding an average sequence for a set of sequences. NLAAF¹⁵ is an exact method to average two sequences using DTW. For more than two sequences, the problem is related to the one of the multiple alignment and requires heuristics. DBA¹⁶ is currently a reference method to average a set of sequences consistently with DTW. COMASA¹⁷ efficiently randomizes the search for the average sequence, using DBA as a local optimization process.

Supervised learning

A nearest-neighbour classifier can achieve state-of-the-art performance when using dynamic time warping as a distance measure.¹⁸

Amerced Dynamic Time Warping

Amerced Dynamic Time Warping (ADTW) is a variant of DTW designed to better control DTW’s permissiveness in the alignments that it allows.¹⁹ The windows that classical DTW uses to constrain alignments introduce a step function. Any warping of the path is allowed within the window and none beyond it. In contrast, ADTW employs an additive penalty that is incurred each time that the path is warped. Any amount of warping is allowed, but each warping action incurs a direct penalty. ADTW significantly outperforms DTW with windowing when applied as a nearest neighbor classifier on a set of benchmark time series classification tasks.¹⁹

Alternative approaches

In functional data analysis, time series are regarded as discretizations of smooth (differentiable) functions of time. By viewing the observed samples at smooth functions, one can utilize continuous mathematics for analyzing data.²⁰ Smoothness and monotonicity of time warp functions may be obtained for instance by integrating a time-varying radial basis function, thus being a one-dimensional diffeomorphism.²¹ Optimal nonlinear time warping functions are computed by minimizing a measure of distance of the set of functions to their warped average. Roughness penalty terms for the warping functions may be added, e.g., by constraining the size of their curvature. The resultant warping functions are smooth, which facilitates further processing. This approach has been successfully applied to analyze patterns and variability of speech movements.²²²³

Another related approach are hidden Markov models (HMM) and it has been shown that the Viterbi algorithm used to search for the most likely path through the HMM is equivalent to stochastic DTW.²⁴²⁵²⁶

DTW and related warping methods are typically used as pre- or post-processing steps in data analyses. If the observed sequences contain both random variation in both their values, shape of observed sequences and random temporal misalignment, the warping may overfit to noise leading to biased results. A simultaneous model formulation with random variation in both values (vertical) and time-parametrization (horizontal) is an example of a nonlinear mixed-effects model.²⁷ In human movement analysis, simultaneous nonlinear mixed-effects modeling has been shown to produce superior results compared to DTW.²⁸

Open-source software

• The tempo C++ library with Python bindings implements Early Abandoned and Pruned DTW as well as Early Abandoned and Pruned ADTW and DTW lower bounds LB_Keogh, LB_Enhanced and LB_Webb.
• The UltraFastMPSearch Java library implements the UltraFastWWSearch algorithm²⁹ for fast warping window tuning.
• The lbimproved C++ library implements Fast Nearest-Neighbor Retrieval algorithms under the GNU General Public License (GPL). It also provides a C++ implementation of dynamic time warping, as well as various lower bounds.
• The FastDTW library is a Java implementation of DTW and a FastDTW implementation that provides optimal or near-optimal alignments with an O(N) time and memory complexity, in contrast to the O(N²) requirement for the standard DTW algorithm. FastDTW uses a multilevel approach that recursively projects a solution from a coarser resolution and refines the projected solution.
• FastDTW fork (Java) published to Maven Central.
• time-series-classification (Java) a package for time series classification using DTW in Weka.
• The DTW suite provides Python (dtw-python) and R packages (dtw) with a comprehensive coverage of the DTW algorithm family members, including a variety of recursion rules (also called step patterns), constraints, and substring matching.
• The mlpy Python library implements DTW.
• The pydtw Python library implements the Manhattan and Euclidean flavoured DTW measures including the LB_Keogh lower bounds.
• The cudadtw C++/CUDA library implements subsequence alignment of Euclidean-flavoured DTW and z-normalized Euclidean distance similar to the popular UCR-Suite on CUDA-enabled accelerators.
• The JavaML machine learning library implements DTW.
• The ndtw C# library implements DTW with various options.
• Sketch-a-Char uses Greedy DTW (implemented in JavaScript) as part of LaTeX symbol classifier program.
• The MatchBox implements DTW to match mel-frequency cepstral coefficients of audio signals.
• Sequence averaging: a GPL Java implementation of DBA.¹⁶
• The Gesture Recognition Toolkit|GRT C++ real-time gesture-recognition toolkit implements DTW.
• The PyHubs software package implements DTW and nearest-neighbour classifiers, as well as their extensions (hubness-aware classifiers).
• The simpledtw Python library implements the classic O(NM) Dynamic Programming algorithm and bases on Numpy. It supports values of any dimension, as well as using custom norm functions for the distances. It is licensed under the MIT license.
• The tslearn Python library implements DTW in the time-series context.
• The cuTWED CUDA Python library implements a state of the art improved Time Warp Edit Distance using only linear memory with phenomenal speedups.
• DynamicAxisWarping.jl Is a Julia implementation of DTW and related algorithms such as FastDTW, SoftDTW, GeneralDTW and DTW barycenters.
• The Multi_DTW implements DTW to match two 1-D arrays or 2-D speech files (2-D array).
• The dtwParallel (Python) package incorporates the main functionalities available in current DTW libraries and novel functionalities such as parallelization, computation of similarity (kernel-based) values, and consideration of data with different types of features (categorical, real-valued, etc.).³⁰

Spoken-word recognition

Due to different speaking rates, a non-linear fluctuation occurs in speech pattern versus time axis, which needs to be eliminated.³¹ DP matching is a pattern-matching algorithm based on dynamic programming (DP), which uses a time-normalization effect, where the fluctuations in the time axis are modeled using a non-linear time-warping function. Considering any two speech patterns, we can get rid of their timing differences by warping the time axis of one so that the maximal coincidence is attained with the other. Moreover, if the warping function is allowed to take any possible value, very less^[clarify] distinction can be made between words belonging to different categories. So, to enhance the distinction between words belonging to different categories, restrictions were imposed on the warping function slope.

Correlation power analysis

Unstable clocks are used to defeat naive power analysis. Several techniques are used to counter this defense, one of which is dynamic time warping.

Finance and econometrics

Dynamic time warping is used in finance and econometrics to assess the quality of the prediction versus real-world data.³²³³³⁴

• Levenshtein distance
• Elastic matching
• Sequence alignment
• Multiple sequence alignment
• Wagner–Fischer algorithm
• Needleman–Wunsch algorithm
• Fréchet distance
• Nonlinear mixed-effects model

• Pavel Senin, Dynamic Time Warping Algorithm Review
• Vintsyuk, T. K. (1968). “Speech discrimination by dynamic programming”. Kibernetika. 4: 81–88.
• Sakoe, H.; Chiba (1978). “Dynamic programming algorithm optimization for spoken word recognition”. IEEE Transactions on Acoustics, Speech, and Signal Processing. 26 (1): 43–49. doi:10.1109/tassp.1978.1163055. S2CID 17900407.
• Myers, C. S.; Rabiner, L. R. (1981). “A Comparative Study of Several Dynamic Time-Warping Algorithms for Connected-Word Recognition”. Bell System Technical Journal. 60 (7): 1389–1409. doi:10.1002/j.1538-7305.1981.tb00272.x. ISSN 0005-8580. S2CID 12857347.
• Rabiner, Lawrence; Juang, Biing-Hwang (1993). “Chapter 4: Pattern-Comparison Techniques”. Fundamentals of speech recognition. Englewood Cliffs, N.J.: PTR Prentice Hall. ISBN 978-0-13-015157-5.
• Müller, Meinard (2007). Dynamic Time Warping. In Information Retrieval for Music and Motion, chapter 4, pages 69-84 (PDF). Springer. doi:10.1007/978-3-540-74048-3. ISBN 978-3-540-74047-6.
• Rakthanmanon, Thanawin (September 2013). “Addressing Big Data Time Series: Mining Trillions of Time Series Subsequences Under Dynamic Time Warping”. ACM Transactions on Knowledge Discovery from Data. 7 (3): 10:1–10:31. doi:10.1145/2513092.2500489. PMC 6790126. PMID 31607834.

Footnotes

1. Olsen, NL; Markussen, B; Raket, LL (2018), “Simultaneous inference for misaligned multivariate functional data”, Journal of the Royal Statistical Society, Series C, 67 (5): 1147–76, arXiv:1606.03295, doi:10.1111/rssc.12276, S2CID 88515233 ↩

2. Gold, Omer; Sharir, Micha (2018). “Dynamic Time Warping and Geometric Edit Distance: Breaking the Quadratic Barrier”. ACM Transactions on Algorithms. 14 (4). doi:10.1145/3230734. S2CID 52070903. ↩

3. Bringmann, Karl; Künnemann, Marvin (2015). “Quadratic Conditional Lower Bounds for String Problems and Dynamic Time Warping”. 2015 IEEE 56th Annual Symposium on Foundations of Computer Science. pp. 79–97. arXiv:1502.01063. doi:10.1109/FOCS.2015.15. ISBN 978-1-4673-8191-8. S2CID 1308171. ↩

4. Abboud, Amir; Backurs, Arturs; Williams, Virginia Vassilevska (2015). “Tight Hardness Results for LCS and Other Sequence Similarity Measures”. 2015 IEEE 56th Annual Symposium on Foundations of Computer Science. pp. 59–78. doi:10.1109/FOCS.2015.14. ISBN 978-1-4673-8191-8. S2CID 16094517. ↩

5. Silva, D. F., Batista, G. E. A. P. A. (2015). Speeding Up All-Pairwise Dynamic Time Warping Matrix Calculation. ↩

6. Al-Naymat, G., Chawla, S., Taheri, J. (2012). SparseDTW: A Novel Approach to Speed up Dynamic Time Warping. ↩

7. Stan Salvador, Philip Chan, FastDTW: Toward Accurate Dynamic Time Warping in Linear Time and Space. KDD Workshop on Mining Temporal and Sequential Data, pp. 70–80, 2004. ↩

8. Meinard Müller, Henning Mattes, and Frank Kurth (2006). An Efficient Multiscale Approach to Audio Synchronization. Proceedings of the International Conference on Music Information Retrieval (ISMIR), pp. 192—197. ↩

9. Thomas Prätzlich, Jonathan Driedger, and Meinard Müller (2016). Memory-Restricted Multiscale Dynamic Time Warping. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), pp. 569—573. ↩

10. Keogh, E.; Ratanamahatana, C. A. (2005). “Exact indexing of dynamic time warping”. Knowledge and Information Systems. 7 (3): 358–386. doi:10.1007/s10115-004-0154-9. S2CID 207056701. ↩

11. Lemire, D. (2009). “Faster Retrieval with a Two-Pass Dynamic-Time-Warping Lower Bound”. Pattern Recognition. 42 (9): 2169–2180. arXiv:0811.3301. Bibcode:2009PatRe..42.2169L. doi:10.1016/j.patcog.2008.11.030. S2CID 8658213. ↩

12. Webb, Geoffrey I.; Petitjean, Francois (2021). “Tight lower bounds for Dynamic Time Warping”. Pattern Recognition. 115: 107895. arXiv:2102.07076. Bibcode:2021PatRe.11507895W. doi:10.1016/j.patcog.2021.107895. S2CID 231925247. ↩ ↩²

13. Wang, Xiaoyue; et al. (2010). “Experimental comparison of representation methods and distance measures for time series data”. Data Mining and Knowledge Discovery. 2010: 1–35. arXiv:1012.2789. ↩

14. Tan, Chang Wei; Petitjean, Francois; Webb, Geoffrey I. (2019). “Elastic bands across the path: A new framework and method to lower bound DTW”. Proceedings of the 2019 SIAM International Conference on Data Mining. pp. 522–530. arXiv:1808.09617. doi:10.1137/1.9781611975673.59. ISBN 978-1-61197-567-3. S2CID 52120426. ↩

15. Gupta, L.; Molfese, D. L.; Tammana, R.; Simos, P. G. (1996). “Nonlinear alignment and averaging for estimating the evoked potential”. IEEE Transactions on Biomedical Engineering. 43 (4): 348–356. doi:10.1109/10.486255. PMID 8626184. S2CID 28688330. ↩

16. Petitjean, F. O.; Ketterlin, A.; Gançarski, P. (2011). “A global averaging method for dynamic time warping, with applications to clustering”. Pattern Recognition. 44 (3): 678. Bibcode:2011PatRe..44..678P. doi:10.1016/j.patcog.2010.09.013. ↩ ↩²

17. Petitjean, F. O.; Gançarski, P. (2012). “Summarizing a set of time series by averaging: From Steiner sequence to compact multiple alignment”. Theoretical Computer Science. 414: 76–91. doi:10.1016/j.tcs.2011.09.029. ↩

18. Ding, Hui; Trajcevski, Goce; Scheuermann, Peter; Wang, Xiaoyue; Keogh, Eamonn (2008). “Querying and mining of time series data: experimental comparison of representations and distance measures”. Proc. VLDB Endow. 1 (2): 1542–1552. doi:10.14778/1454159.1454226. ↩

19. Herrmann, Matthieu; Webb, Geoffrey I. (2023). “Amercing: An intuitive and effective constraint for dynamic time warping”. Pattern Recognition. 137: 109333. Bibcode:2023PatRe.13709333H. doi:10.1016/j.patcog.2023.109333. S2CID 256182457. ↩ ↩²

20. Lucero, J. C.; Munhall, K. G.; Gracco, V. G.; Ramsay, J. O. (1997). “On the Registration of Time and the Patterning of Speech Movements”. Journal of Speech, Language, and Hearing Research. 40 (5): 1111–1117. doi:10.1044/jslhr.4005.1111. PMID 9328881. ↩

21. Durrleman, S; Pennec, X.; Trouvé, A.; Braga, J.; Gerig, G. & Ayache, N. (2013). “Toward a Comprehensive Framework for the Spatiotemporal Statistical Analysis of Longitudinal Shape Data”. International Journal of Computer Vision. 103 (1): 22–59. doi:10.1007/s11263-012-0592-x. PMC 3744347. PMID 23956495. ↩

22. Howell, P.; Anderson, A.; Lucero, J. C. (2010). “Speech motor timing and fluency”. In Maassen, B.; van Lieshout, P. (eds.). Speech Motor Control: New Developments in Basic and Applied Research. Oxford University Press. pp. 215–225. ISBN 978-0199235797. ↩

23. Koenig, Laura L.; Lucero, Jorge C.; Perlman, Elizabeth (2008). “Speech production variability in fricatives of children and adults: Results of functional data analysis”. The Journal of the Acoustical Society of America. 124 (5): 3158–3170. Bibcode:2008ASAJ..124.3158K. doi:10.1121/1.2981639. ISSN 0001-4966. PMC 2677351. PMID 19045800. ↩

24. Nakagawa, Seiichi; Nakanishi, Hirobumi (1988-01-01). “Speaker-Independent English Consonant and Japanese Word Recognition by a Stochastic Dynamic Time Warping Method”. IETE Journal of Research. 34 (1): 87–95. doi:10.1080/03772063.1988.11436710. ISSN 0377-2063. ↩

25. Fang, Chunsheng. “From Dynamic Time Warping (DTW) to Hidden Markov Model (HMM)” (PDF). ↩

26. Juang, B. H. (September 1984). “On the hidden Markov model and dynamic time warping for speech recognitionx2014; A unified view”. AT&T Bell Laboratories Technical Journal. 63 (7): 1213–1243. doi:10.1002/j.1538-7305.1984.tb00034.x. ISSN 0748-612X. S2CID 8461145. ↩

27. Raket LL, Sommer S, Markussen B (2014). “A nonlinear mixed-effects model for simultaneous smoothing and registration of functional data”. Pattern Recognition Letters. 38: 1–7. Bibcode:2014PaReL..38…1R. doi:10.1016/j.patrec.2013.10.018. ↩

28. Raket LL, Grimme B, Schöner G, Igel C, Markussen B (2016). “Separating timing, movement conditions and individual differences in the analysis of human movement”. PLOS Computational Biology. 12 (9): e1005092. arXiv:1601.02775. Bibcode:2016PLSCB..12E5092R. doi:10.1371/journal.pcbi.1005092. PMC 5033575. PMID 27657545. ↩

29. Tan, Chang Wei; Herrmann, Matthieu; Webb, Geoffrey I. (2021). “Ultra fast warping window optimization for Dynamic Time Warping” (PDF). 2021 IEEE International Conference on Data Mining (ICDM). pp. 589–598. doi:10.1109/ICDM51629.2021.00070. ISBN 978-1-6654-2398-4. S2CID 246291550. ↩

30. Escudero-Arnanz, Óscar; Marques, Antonio G; Soguero-Ruiz, Cristina; Mora-Jiménez, Inmaculada; Robles, Gregorio (2023). “dtwParallel: A Python package to efficiently compute dynamic time warping between time series”. SoftwareX. 22 (101364). Bibcode:2023SoftX..2201364E. doi:10.1016/J.SOFTX.2023.101364. hdl:10115/24752. Retrieved 2024-12-06. ↩

31. Sakoe, Hiroaki; Chiba, Seibi (1978). “Dynamic programming algorithm optimization for spoken word recognition”. IEEE Transactions on Acoustics, Speech, and Signal Processing. 26 (1): 43–49. doi:10.1109/tassp.1978.1163055. S2CID 17900407. ↩

32. Orlando, Giuseppe; Bufalo, Michele; Stoop, Ruedi (2022-02-01). “Financial markets’ deterministic aspects modeled by a low-dimensional equation”. Scientific Reports. 12 (1): 1693. Bibcode:2022NatSR..12.1693O. doi:10.1038/s41598-022-05765-z. ISSN 2045-2322. PMC 8807815. PMID 35105929. ↩

33. Mastroeni, Loretta; Mazzoccoli, Alessandro; Quaresima, Greta; Vellucci, Pierluigi (2021-02-01). “Decoupling and recoupling in the crude oil price benchmarks: An investigation of similarity patterns”. Energy Economics. 94: 105036. Bibcode:2021EneEc..9405036M. doi:10.1016/j.eneco.2020.105036. ISSN 0140-9883. S2CID 230536868. ↩

34. Orlando, Giuseppe; Bufalo, Michele (2021-12-10). “Modelling bursts and chaos regularization in credit risk with a deterministic nonlinear model”. Finance Research Letters. 47: 102599. doi:10.1016/j.frl.2021.102599. ISSN 1544-6123. ↩