Attention sinks from the graph perspective - the-tensor-throne - Obsidian Publish

Attention sinks have recently come back to the forefront of architecture discussion, especially due to their appearance in gpt-oss (although in a different form than the effect we’re discussing today).

As a mechanism, attention sinks are easy to describe: when trained, decoder-only transformer models tend to allocate a disproportionate amount of attention to the first few tokens, and especially to the first.

This effect is well studied in its practical terms, and is often attributed to the model “offloading” probability mass to the early tokens to avoid their spurious allocation elsewhere. Recent works, like Softpick, provide architectural choices that prevent sinks from forming. While this explanation may sound convincing at a first glance, my intuition is still bothered by it: what do you mean the model “offloads”? Of course it doesn’t explore that possibility intentionally, there must be some mechanism by which the attention sinks are either advantageous or a result of an intrinsic bias to the model. In this blogpost, we will argue that there is a significant bias in decoder-only transformers that may be to blame, at least partially, for this phenomenon. Moreover, this will also allow us to introduce a series of blogposts focused on analyzing transformers from the lens of message passing on graphs.

Attention as message-passing 

Recent work by Chaitanya K. Joshi has finally freed us from having to formalize independently a well known property of Transformers (and especially of attention layers): them being a special case of Graph Neural Networks (just like pretty much anything else, to be fair).

As as setting to our discussion, though, we will go over another angle with which attention can be seen as message-passing on a graph.

Most people are usually introduced to (multi-headed) self-attention directly via the attention is all you need paper. Despite this being generally a good practice in my opinion, it generally directs attention to being interpreted as the simplest way of making tokens interact in a transformer, or as just a soft version of a dictionary lookup. While neither being wrong, such interpretations often drown out some interesting geometric details that lie in attention itself.

Let’s start with regular, multiheaded attention.

Say you have  tokens, with an embedding dimension .

Let our input tokens be shaped as a matrix , we first process  with three different linear projections, namely  ,  and , and end up with the respective ,  and   matrices.

We then perform the well-known attention operation

let’s take a look at .
If we rewrite it component-wise we get

and if we note that  and ‘s rows, respectively  and , we see that

the attention matrix ‘s entries are thus simply speaking the euclidean dot product between token embeddings, projected via the query and key matrices.

This still falls within the classical presentation of attention, so nothing to see here as of yet.

What if we could reinterpret these operations from a more geometric/topological perspective?
Let’s take, for example

And let’s treat the rows of (X) as a point‑cloud:

Constructing the ,, matrices for attention, we effectively project that cloud in three ways

We use these distinct projections to capture a graph-like structure, building an adjacency matrix between tokens, which can be seen as nodes

Stacking all scores:

The intuition is: the more points align in Query - Key space, the stronger their connection will be, and hence the stronger the link between the nodes.

Finally, we use softmax to normalize outgoing weights from each node

Each row of  is a probability distribution and corresponds to the node’s neighbors; small logits shrink toward 0, meaning most edge weights are very close to zero, apart from a few. This effectively heavily sparsifies the neighborhood, assigning most of the link weights to just a few connections, while the rest go to zero.

Lastly, the final operation

can now be interpreted from an interesting perspective:  can be seen as a vector-valued function defined on nodes of the graphs.

If we write it row-wise (hence focusing on each token, or node, at a time), we see that the updated function’s value associated with the node becomes

But what does multiplying a function defined on a graph by the adjacency mean? Let’s say we have a directed graph  with adjacency , with a function  and .
Then, the multiplicationcan be written, component-wise, as

Remember that, for an adjacency matrix, elements of column  represent incoming links from other nodes in the graph. This means that , or the result of the adjacency-multiplied function , is the weighted average of  over incoming nodes to node i, where the weights are decided by the adjacency matrix’ entries. Intuitively, you can think of this process as a sort of diffusion: features are aggregates of their neighbours. This means that, if we start with a rather unequally spatially distributed function (say a very localized highly positive region, and the rest being zero), then nodes on the boundary of the highly positive region would “diffuse” the highly positive values towards neighbouring nodes. Of course the topology of the graph heavily influences the speed of this diffusion. Unsurprisingly, this ties back very well with the actual physical phenomenon of heat diffusion, as we will see in a future blogpost.

Causal Transformers and Attention Sinks 

Note that the discussion so far has been agnostic of masking strategies applied to the attention score. While several uses of Transformer models employ attention bidirectionally, LLMs, our Large Model protagonists, are usually causally masking attention to leverage parallelism for their Next Token Prediction task.

In our attention mechanism, this is done by substituting our  adjacency matrix with a masked, causal one, in the shape of , with  if  and zero otherwise. Note that this gives our attention graph an even more interesting structure: our graph is now, by design, a Directed Acyclic Graph (DAG), meaning the graph contains no loops, and its adjacency matrix is nilpotent (meaning there exists  such that , ).

One interesting corollary of this observation is that adjacency-based diffusion over DAGs is bound to accumulate information in sinks, specifically, in the first tokens of a causal model. This can be made explicit by looking at the shape of powers of :

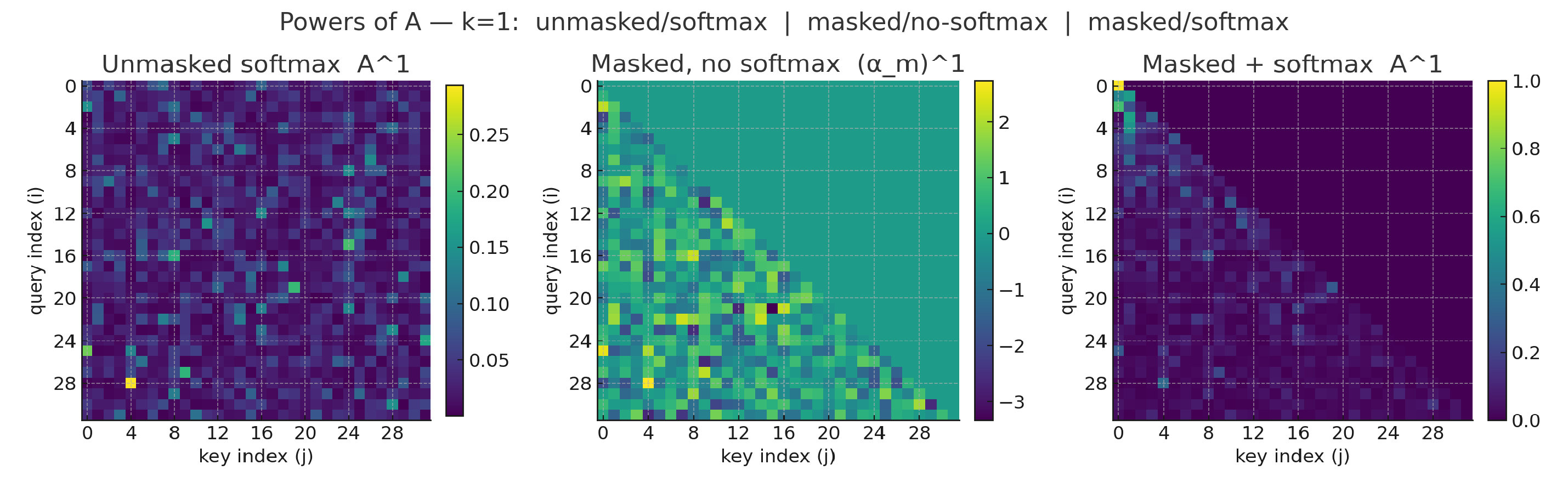
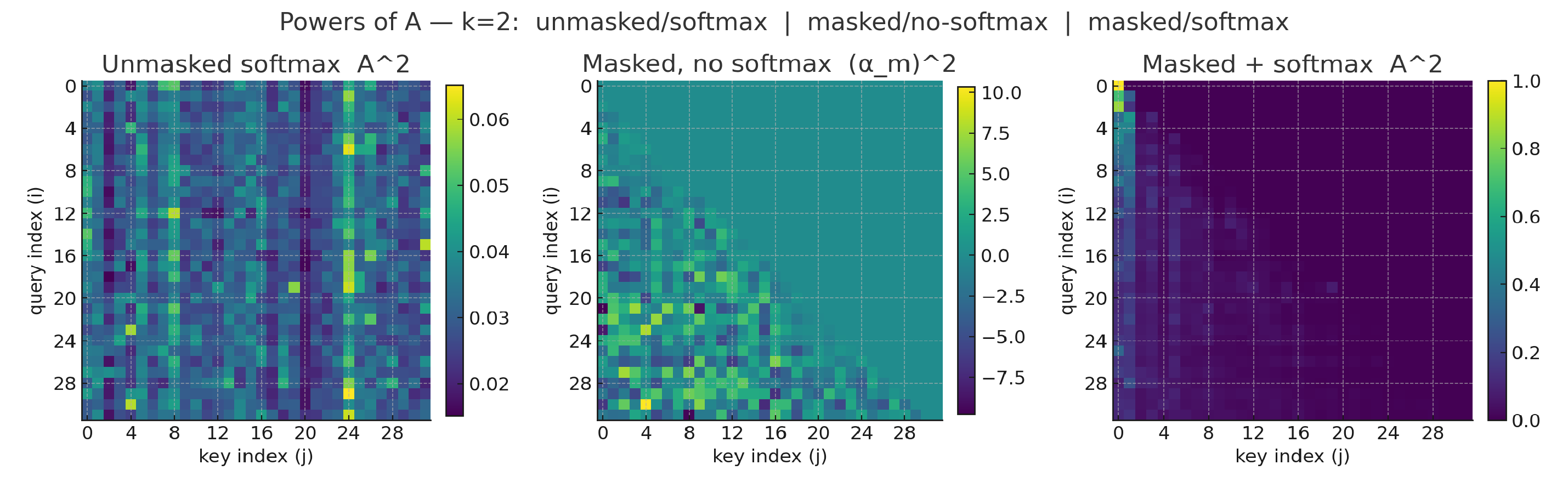
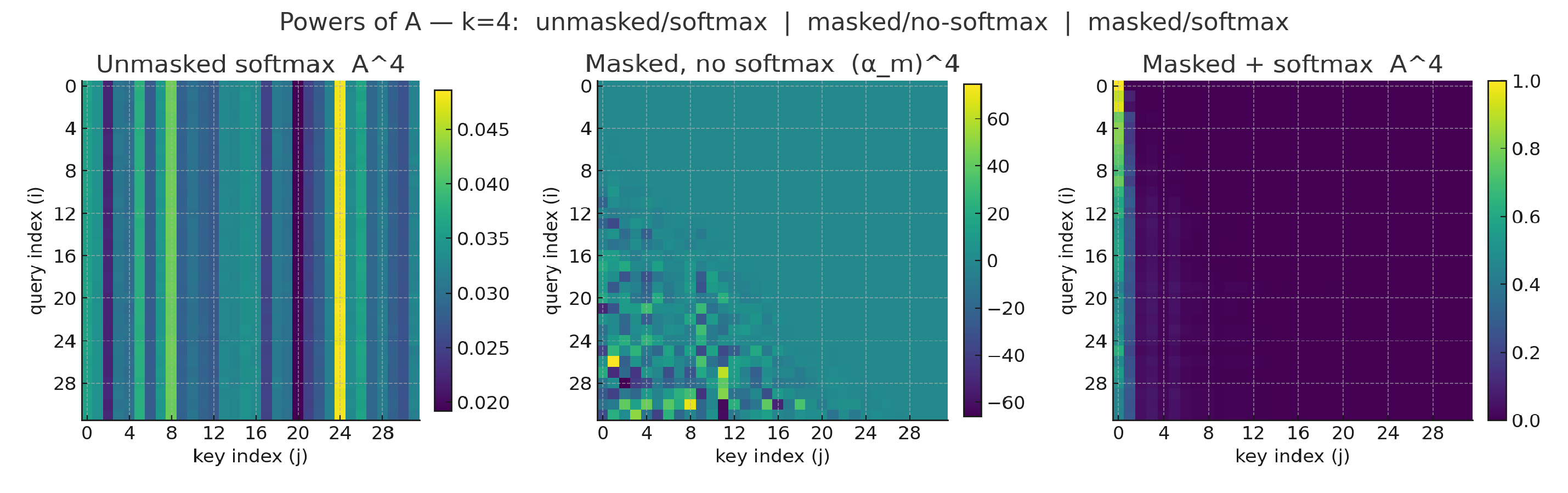
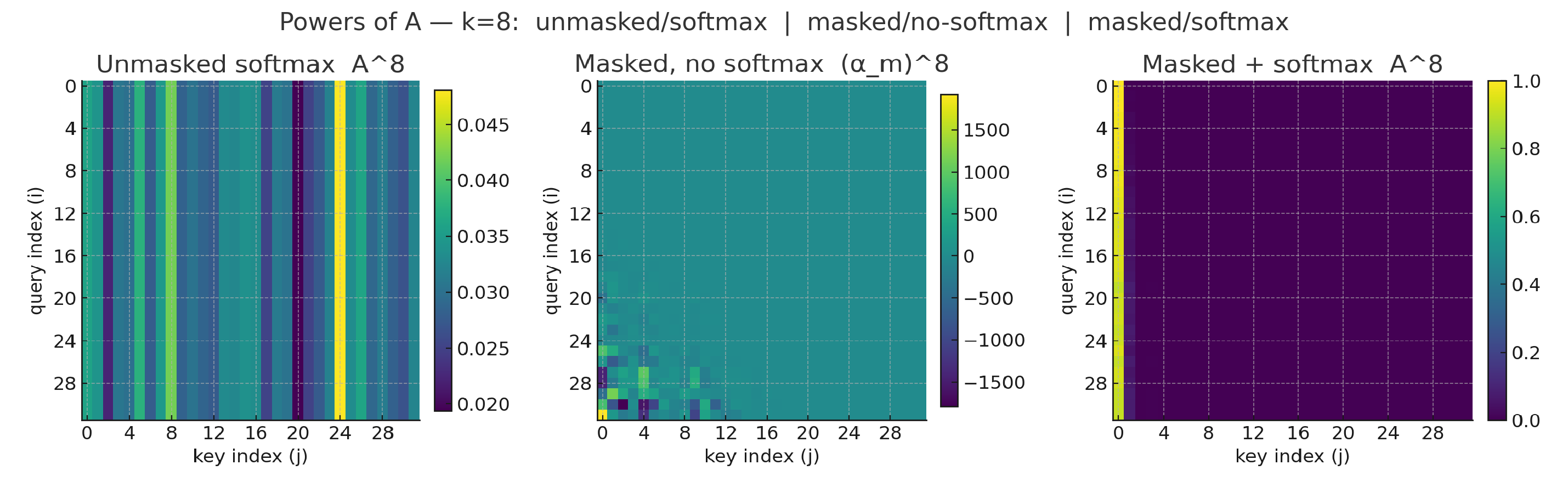
Fig.1-4: we simulate an attention matrix being composed with itself several times, across three different configurations: bidirectional, masked pre-softmax, softmax. As we can see, the combination of masking (making the matrix nilpotent) and softmax (forcing row-wise mass to sum to one) rapidly recovers the familiar attention pattern we see for attention sinks

These plots (Fig.1-4) show exactly what we expect on a DAG: as we take powers of the (masked) attention matrix  the mass moves “leftward” toward early tokens. In the strictly lower-triangular case (no self-loops) this is a nilpotent operator, so sufficiently high powers collapse entirely into the earliest positions.

To connect this with learning dynamics, linearize one residual attention block (one head, for intuition; treat the MLP as a node-wise map) as

Stacking (L) such blocks yields an end-to-end map that is a polynomial in the ()’s:

When the  are geometrically similar across depth, dominant terms behave like powers of a causal . That is the same “multi-hop diffusion” we saw in the previous figures, progressively concentrating influence onto the first columns (early tokens).

But if that’s the case during a forward pass, what makes a model exhibit this bias in across training, as it’s been noticed in the literature?

As it turns out, backprop itself mirrors this geometry. Gradients w.r.t. hidden states propagate with Jacobian transposes along the value path:

Hence token-wise gradients accumulate along column sums of products of  (or, equivalently, row sums of products of ). In a causal DAG those column sums are largest for earlier positions, so both activations and gradients preferentially route through (and update) paths that point to early tokens.

Practically, residual connections make the map a polynomial (not a single ), multi-head mixing and  projections reshape directions, and layer-norm rescales signals. But the structural bias remains: deeper layers inherit updates that look like compositions of attention-diffusion steps, which, under causal masking, tend to be more and more “first-column concentrated”.

Another corollary of our observation is that it would suggest that later layers are more subject to the attention sink phenomenon, while the very first layer should be much less impacted. This turns out to be true and well known when studying attention sinks, as is the case, for example, for LLama2, or in this paper and this one.

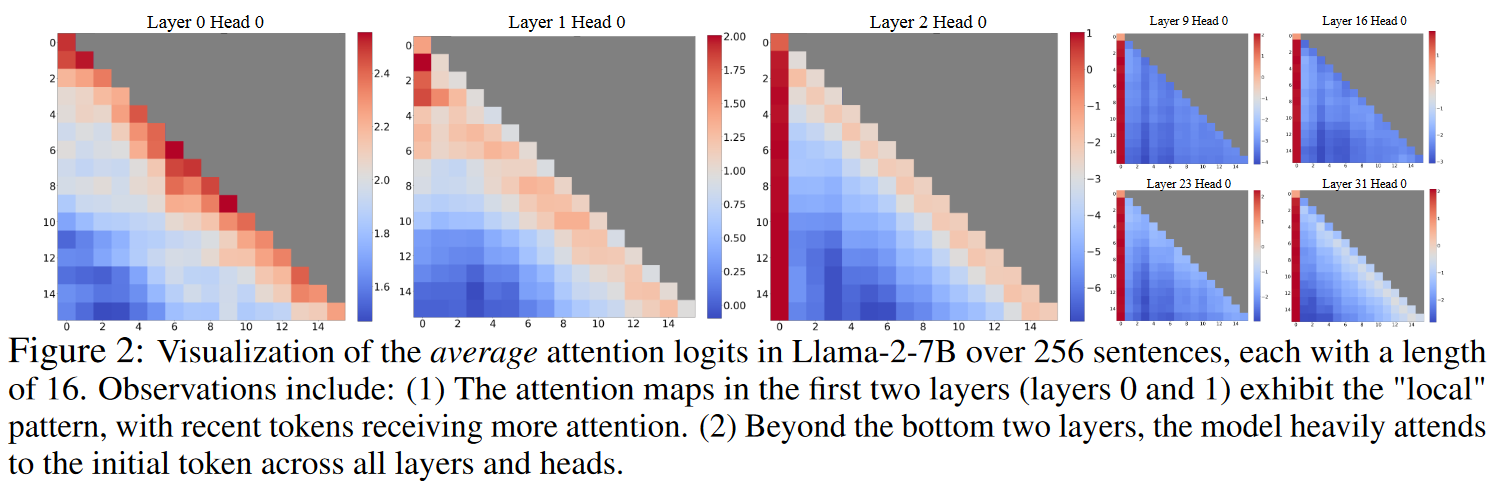
Note that, while this may not be the single effect responsible for attention sinks, this means we should expect any causal decoder-only transformer to exihibit a bias towards allocating attention to its first few tokens (and increasingly so to the first).

This fundamentally clashes with many interpretations of sinks: several works characterize them as a useful feature that is learned by the model. If what we propose is true, it’s exactly the opposite: when sinks don’t show up, it means the message-passing mechanism of your transformer is fundamentally flawed, and hence it performs worse.

The attention sinks become a signal of healthy communication of tokens in attention, being a bias that is intrinsic to the causal, decoder-only transformer.

Wrapping up 

So, to recap, what does this mean? We individuated a possible mechanism that may bias Causal Transformers to accumulate attention on its first few tokens. Note that we showed the mechanism in a higly simplified setting, and are proposing the idea that, despite those simplifications, the underlying effect is still strong enough to accumulate across training steps of a large transformer, and eventually explain the existence of attention sink as we know them. In the next blogposts, we will use the same graph-centric framing of attention to analyze the problem of long context in transformer models, connecting it to heat diffusion and the oversmoothing and oversquashing phenomena known in the GNN literature. Stay tuned!

Acknowledgements 

Thanks a lot to thelakosiffers, Niccolò, Fabrizio , Cynde , Francescoand Zed for their precious feedback!

---

Suggested citation 

@misc{pappone2025attentionsinks,  
author = {Francesco Pappone},  
title = {Attention sinks from the graph perspective},  
year = {2025},  
month = {August},  
day = {24},  
institution = {Università La Sapienza di Roma -- PSTP Technoscience},  
howpublished = {\url{[https://publish.obsidian.md/the-tensor-throne/Transformers+as+GNNs/Attention+sinks+from+the+graph+perspective}}](https://publish.obsidian.md/the-tensor-throne/Transformers+as+GNNs/Attention+sinks+from+the+graph+perspective%7D%7D),  
note = {Blogpost}  
}