Fused Softmax — Triton documentation
Excerpt
Note
Note
Go to the end to download the full example code.
In this tutorial, you will write a fused softmax operation that is significantly faster than PyTorch’s native op for a particular class of matrices: those whose rows can fit in the GPU’s SRAM.
In doing so, you will learn about:
-
The benefits of kernel fusion for bandwidth-bound operations.
-
Reduction operators in Triton.
Motivations¶
Custom GPU kernels for elementwise additions are educationally valuable but won’t get you very far in practice. Let us consider instead the case of a simple (numerically stabilized) softmax operation:
<span></span><span>import</span> <span>torch</span>
<span>import</span> <span>triton</span>
<span>import</span> <span>triton.language</span> <span>as</span> <span>tl</span>
<span>from</span> <span>triton.runtime</span> <span>import</span> <span>driver</span>
<span>def</span> <span>is_hip</span><span>():</span>
<span>return</span> <span>triton</span><span>.</span><span>runtime</span><span>.</span><span>driver</span><span>.</span><span>active</span><span>.</span><span>get_current_target</span><span>()</span><span>.</span><span>backend</span> <span>==</span> <span>"hip"</span>
<span>def</span> <span>is_cdna</span><span>():</span>
<span>return</span> <span>is_hip</span><span>()</span> <span>and</span> <span>triton</span><span>.</span><span>runtime</span><span>.</span><span>driver</span><span>.</span><span>active</span><span>.</span><span>get_current_target</span><span>()</span><span>.</span><span>arch</span> <span>in</span> <span>(</span><span>'gfx940'</span><span>,</span> <span>'gfx941'</span><span>,</span> <span>'gfx942'</span><span>,</span>
<span>'gfx90a'</span><span>,</span> <span>'gfx908'</span><span>)</span>
<span>def</span> <span>naive_softmax</span><span>(</span><span>x</span><span>):</span>
<span> </span><span>"""Compute row-wise softmax of X using native pytorch</span>
<span> We subtract the maximum element in order to avoid overflows. Softmax is invariant to</span>
<span> this shift.</span>
<span> """</span>
<span># read MN elements ; write M elements</span>
<span>x_max</span> <span>=</span> <span>x</span><span>.</span><span>max</span><span>(</span><span>dim</span><span>=</span><span>1</span><span>)[</span><span>0</span><span>]</span>
<span># read MN + M elements ; write MN elements</span>
<span>z</span> <span>=</span> <span>x</span> <span>-</span> <span>x_max</span><span>[:,</span> <span>None</span><span>]</span>
<span># read MN elements ; write MN elements</span>
<span>numerator</span> <span>=</span> <span>torch</span><span>.</span><span>exp</span><span>(</span><span>z</span><span>)</span>
<span># read MN elements ; write M elements</span>
<span>denominator</span> <span>=</span> <span>numerator</span><span>.</span><span>sum</span><span>(</span><span>dim</span><span>=</span><span>1</span><span>)</span>
<span># read MN + M elements ; write MN elements</span>
<span>ret</span> <span>=</span> <span>numerator</span> <span>/</span> <span>denominator</span><span>[:,</span> <span>None</span><span>]</span>
<span># in total: read 5MN + 2M elements ; wrote 3MN + 2M elements</span>
<span>return</span> <span>ret</span>
When implemented naively in PyTorch, computing y = naive_softmax(x) for requires reading elements from DRAM and writing back elements. This is obviously wasteful; we’d prefer to have a custom “fused” kernel that only reads X once and does all the necessary computations on-chip. Doing so would require reading and writing back only bytes, so we could expect a theoretical speed-up of ~4x (i.e., ). The torch.jit.script flags aims to perform this kind of “kernel fusion” automatically but, as we will see later, it is still far from ideal.
Compute Kernel¶
Our softmax kernel works as follows: each program loads a set of rows of the input matrix X strided by number of programs, normalizes it and writes back the result to the output Y.
Note that one important limitation of Triton is that each block must have a power-of-two number of elements, so we need to internally “pad” each row and guard the memory operations properly if we want to handle any possible input shapes:
<span></span><span>@triton</span><span>.</span><span>jit</span>
<span>def</span> <span>softmax_kernel</span><span>(</span><span>output_ptr</span><span>,</span> <span>input_ptr</span><span>,</span> <span>input_row_stride</span><span>,</span> <span>output_row_stride</span><span>,</span> <span>n_rows</span><span>,</span> <span>n_cols</span><span>,</span> <span>BLOCK_SIZE</span><span>:</span> <span>tl</span><span>.</span><span>constexpr</span><span>,</span>
<span>num_stages</span><span>:</span> <span>tl</span><span>.</span><span>constexpr</span><span>):</span>
<span># starting row of the program</span>
<span>row_start</span> <span>=</span> <span>tl</span><span>.</span><span>program_id</span><span>(</span><span>0</span><span>)</span>
<span>row_step</span> <span>=</span> <span>tl</span><span>.</span><span>num_programs</span><span>(</span><span>0</span><span>)</span>
<span>for</span> <span>row_idx</span> <span>in</span> <span>tl</span><span>.</span><span>range</span><span>(</span><span>row_start</span><span>,</span> <span>n_rows</span><span>,</span> <span>row_step</span><span>,</span> <span>num_stages</span><span>=</span><span>num_stages</span><span>):</span>
<span># The stride represents how much we need to increase the pointer to advance 1 row</span>
<span>row_start_ptr</span> <span>=</span> <span>input_ptr</span> <span>+</span> <span>row_idx</span> <span>*</span> <span>input_row_stride</span>
<span># The block size is the next power of two greater than n_cols, so we can fit each</span>
<span># row in a single block</span>
<span>col_offsets</span> <span>=</span> <span>tl</span><span>.</span><span>arange</span><span>(</span><span>0</span><span>,</span> <span>BLOCK_SIZE</span><span>)</span>
<span>input_ptrs</span> <span>=</span> <span>row_start_ptr</span> <span>+</span> <span>col_offsets</span>
<span># Load the row into SRAM, using a mask since BLOCK_SIZE may be > than n_cols</span>
<span>mask</span> <span>=</span> <span>col_offsets</span> <span><</span> <span>n_cols</span>
<span>row</span> <span>=</span> <span>tl</span><span>.</span><span>load</span><span>(</span><span>input_ptrs</span><span>,</span> <span>mask</span><span>=</span><span>mask</span><span>,</span> <span>other</span><span>=-</span><span>float</span><span>(</span><span>'inf'</span><span>))</span>
<span># Subtract maximum for numerical stability</span>
<span>row_minus_max</span> <span>=</span> <span>row</span> <span>-</span> <span>tl</span><span>.</span><span>max</span><span>(</span><span>row</span><span>,</span> <span>axis</span><span>=</span><span>0</span><span>)</span>
<span># Note that exponentiation in Triton is fast but approximate (i.e., think __expf in CUDA)</span>
<span>numerator</span> <span>=</span> <span>tl</span><span>.</span><span>exp</span><span>(</span><span>row_minus_max</span><span>)</span>
<span>denominator</span> <span>=</span> <span>tl</span><span>.</span><span>sum</span><span>(</span><span>numerator</span><span>,</span> <span>axis</span><span>=</span><span>0</span><span>)</span>
<span>softmax_output</span> <span>=</span> <span>numerator</span> <span>/</span> <span>denominator</span>
<span># Write back output to DRAM</span>
<span>output_row_start_ptr</span> <span>=</span> <span>output_ptr</span> <span>+</span> <span>row_idx</span> <span>*</span> <span>output_row_stride</span>
<span>output_ptrs</span> <span>=</span> <span>output_row_start_ptr</span> <span>+</span> <span>col_offsets</span>
<span>tl</span><span>.</span><span>store</span><span>(</span><span>output_ptrs</span><span>,</span> <span>softmax_output</span><span>,</span> <span>mask</span><span>=</span><span>mask</span><span>)</span>
We can create a helper function that enqueues the kernel and its (meta-)arguments for any given input tensor.
<span></span><span>device</span> <span>=</span> <span>torch</span><span>.</span><span>cuda</span><span>.</span><span>current_device</span><span>()</span>
<span>properties</span> <span>=</span> <span>driver</span><span>.</span><span>active</span><span>.</span><span>utils</span><span>.</span><span>get_device_properties</span><span>(</span><span>device</span><span>)</span>
<span>NUM_SM</span> <span>=</span> <span>properties</span><span>[</span><span>"multiprocessor_count"</span><span>]</span>
<span>NUM_REGS</span> <span>=</span> <span>properties</span><span>[</span><span>"max_num_regs"</span><span>]</span>
<span>SIZE_SMEM</span> <span>=</span> <span>properties</span><span>[</span><span>"max_shared_mem"</span><span>]</span>
<span>WARP_SIZE</span> <span>=</span> <span>properties</span><span>[</span><span>"warpSize"</span><span>]</span>
<span>target</span> <span>=</span> <span>triton</span><span>.</span><span>runtime</span><span>.</span><span>driver</span><span>.</span><span>active</span><span>.</span><span>get_current_target</span><span>()</span>
<span>kernels</span> <span>=</span> <span>{}</span>
<span>def</span> <span>softmax</span><span>(</span><span>x</span><span>):</span>
<span>n_rows</span><span>,</span> <span>n_cols</span> <span>=</span> <span>x</span><span>.</span><span>shape</span>
<span># The block size of each loop iteration is the smallest power of two greater than the number of columns in `x`</span>
<span>BLOCK_SIZE</span> <span>=</span> <span>triton</span><span>.</span><span>next_power_of_2</span><span>(</span><span>n_cols</span><span>)</span>
<span># Another trick we can use is to ask the compiler to use more threads per row by</span>
<span># increasing the number of warps (`num_warps`) over which each row is distributed.</span>
<span># You will see in the next tutorial how to auto-tune this value in a more natural</span>
<span># way so you don't have to come up with manual heuristics yourself.</span>
<span>num_warps</span> <span>=</span> <span>8</span>
<span># Number of software piepling stages.</span>
<span>num_stages</span> <span>=</span> <span>4</span> <span>if</span> <span>SIZE_SMEM</span> <span>></span> <span>200000</span> <span>else</span> <span>2</span>
<span># Allocate output</span>
<span>y</span> <span>=</span> <span>torch</span><span>.</span><span>empty_like</span><span>(</span><span>x</span><span>)</span>
<span># pre-compile kernel to get register usage and compute thread occupancy.</span>
<span>kernel</span><span>,</span> <span>num_programs</span> <span>=</span> <span>kernels</span><span>.</span><span>get</span><span>(</span><span>BLOCK_SIZE</span><span>,</span> <span>(</span><span>None</span><span>,</span> <span>0</span><span>))</span>
<span>if</span> <span>kernel</span> <span>is</span> <span>None</span><span>:</span>
<span>kernel</span> <span>=</span> <span>softmax_kernel</span><span>.</span><span>warmup</span><span>(</span><span>y</span><span>,</span> <span>x</span><span>,</span> <span>x</span><span>.</span><span>stride</span><span>(</span><span>0</span><span>),</span> <span>y</span><span>.</span><span>stride</span><span>(</span><span>0</span><span>),</span> <span>n_rows</span><span>,</span> <span>n_cols</span><span>,</span> <span>BLOCK_SIZE</span><span>=</span><span>BLOCK_SIZE</span><span>,</span>
<span>num_stages</span><span>=</span><span>num_stages</span><span>,</span> <span>num_warps</span><span>=</span><span>num_warps</span><span>,</span> <span>grid</span><span>=</span><span>(</span><span>1</span><span>,</span> <span>))</span>
<span>kernel</span><span>.</span><span>_init_handles</span><span>()</span>
<span>n_regs</span> <span>=</span> <span>kernel</span><span>.</span><span>n_regs</span>
<span>size_smem</span> <span>=</span> <span>kernel</span><span>.</span><span>metadata</span><span>.</span><span>shared</span>
<span>if</span> <span>is_hip</span><span>():</span>
<span># NUM_REGS represents the number of regular purpose registers. On CDNA architectures this is half of all registers available.</span>
<span># However, this is not always the case. In most cases all registers can be used as regular purpose registers.</span>
<span># ISA SECTION (3.6.4 for CDNA3)</span>
<span># VGPRs are allocated out of two pools: regular VGPRs and accumulation VGPRs. Accumulation VGPRs are used</span>
<span># with matrix VALU instructions, and can also be loaded directly from memory. A wave may have up to 512 total</span>
<span># VGPRs, 256 of each type. When a wave has fewer than 512 total VGPRs, the number of each type is flexible - it is</span>
<span># not required to be equal numbers of both types.</span>
<span>if</span> <span>is_cdna</span><span>():</span>
<span>NUM_GPRS</span> <span>=</span> <span>NUM_REGS</span> <span>*</span> <span>2</span>
<span># MAX_NUM_THREADS represents maximum number of resident threads per multi-processor.</span>
<span># When we divide this number with WARP_SIZE we get maximum number of waves that can</span>
<span># execute on a CU (multi-processor) in parallel.</span>
<span>MAX_NUM_THREADS</span> <span>=</span> <span>properties</span><span>[</span><span>"max_threads_per_sm"</span><span>]</span>
<span>max_num_waves</span> <span>=</span> <span>MAX_NUM_THREADS</span> <span>//</span> <span>WARP_SIZE</span>
<span>occupancy</span> <span>=</span> <span>min</span><span>(</span><span>NUM_GPRS</span> <span>//</span> <span>WARP_SIZE</span> <span>//</span> <span>n_regs</span><span>,</span> <span>max_num_waves</span><span>)</span> <span>//</span> <span>num_warps</span>
<span>else</span><span>:</span>
<span>occupancy</span> <span>=</span> <span>NUM_REGS</span> <span>//</span> <span>(</span><span>n_regs</span> <span>*</span> <span>WARP_SIZE</span> <span>*</span> <span>num_warps</span><span>)</span>
<span>occupancy</span> <span>=</span> <span>min</span><span>(</span><span>occupancy</span><span>,</span> <span>SIZE_SMEM</span> <span>//</span> <span>size_smem</span><span>)</span>
<span>num_programs</span> <span>=</span> <span>NUM_SM</span> <span>*</span> <span>occupancy</span>
<span>kernels</span><span>[</span><span>BLOCK_SIZE</span><span>]</span> <span>=</span> <span>(</span><span>kernel</span><span>,</span> <span>num_programs</span><span>)</span>
<span>num_programs</span> <span>=</span> <span>min</span><span>(</span><span>num_programs</span><span>,</span> <span>n_rows</span><span>)</span>
<span># Create a number of persistent programs.</span>
<span>kernel</span><span>[(</span><span>num_programs</span><span>,</span> <span>1</span><span>,</span> <span>1</span><span>)](</span>
<span>y</span><span>,</span>
<span>x</span><span>,</span>
<span>x</span><span>.</span><span>stride</span><span>(</span><span>0</span><span>),</span>
<span>y</span><span>.</span><span>stride</span><span>(</span><span>0</span><span>),</span>
<span>n_rows</span><span>,</span>
<span>n_cols</span><span>,</span>
<span>)</span>
<span>return</span> <span>y</span>
Unit Test¶
We make sure that we test our kernel on a matrix with an irregular number of rows and columns. This will allow us to verify that our padding mechanism works.
<span></span><span>torch</span><span>.</span><span>manual_seed</span><span>(</span><span>0</span><span>)</span>
<span>x</span> <span>=</span> <span>torch</span><span>.</span><span>randn</span><span>(</span><span>1823</span><span>,</span> <span>781</span><span>,</span> <span>device</span><span>=</span><span>'cuda'</span><span>)</span>
<span>y_triton</span> <span>=</span> <span>softmax</span><span>(</span><span>x</span><span>)</span>
<span>y_torch</span> <span>=</span> <span>torch</span><span>.</span><span>softmax</span><span>(</span><span>x</span><span>,</span> <span>axis</span><span>=</span><span>1</span><span>)</span>
<span>assert</span> <span>torch</span><span>.</span><span>allclose</span><span>(</span><span>y_triton</span><span>,</span> <span>y_torch</span><span>),</span> <span>(</span><span>y_triton</span><span>,</span> <span>y_torch</span><span>)</span>
As expected, the results are identical.
Benchmark¶
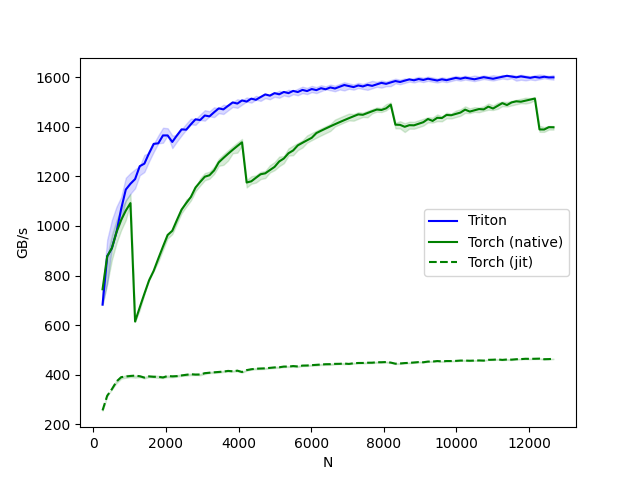
Here we will benchmark our operation as a function of the number of columns in the input matrix – assuming 4096 rows. We will then compare its performance against (1) torch.softmax and (2) the naive_softmax defined above.
<span></span><span>@triton</span><span>.</span><span>testing</span><span>.</span><span>perf_report</span><span>(</span>
<span>triton</span><span>.</span><span>testing</span><span>.</span><span>Benchmark</span><span>(</span>
<span>x_names</span><span>=</span><span>[</span><span>'N'</span><span>],</span> <span># argument names to use as an x-axis for the plot</span>
<span>x_vals</span><span>=</span><span>[</span><span>128</span> <span>*</span> <span>i</span> <span>for</span> <span>i</span> <span>in</span> <span>range</span><span>(</span><span>2</span><span>,</span> <span>100</span><span>)],</span> <span># different possible values for `x_name`</span>
<span>line_arg</span><span>=</span><span>'provider'</span><span>,</span> <span># argument name whose value corresponds to a different line in the plot</span>
<span>line_vals</span><span>=</span><span>[</span><span>'triton'</span><span>,</span> <span>'torch'</span><span>],</span> <span># possible values for `line_arg``</span>
<span>line_names</span><span>=</span><span>[</span>
<span>"Triton"</span><span>,</span>
<span>"Torch"</span><span>,</span>
<span>],</span> <span># label name for the lines</span>
<span>styles</span><span>=</span><span>[(</span><span>'blue'</span><span>,</span> <span>'-'</span><span>),</span> <span>(</span><span>'green'</span><span>,</span> <span>'-'</span><span>)],</span> <span># line styles</span>
<span>ylabel</span><span>=</span><span>"GB/s"</span><span>,</span> <span># label name for the y-axis</span>
<span>plot_name</span><span>=</span><span>"softmax-performance"</span><span>,</span> <span># name for the plot. Used also as a file name for saving the plot.</span>
<span>args</span><span>=</span><span>{</span><span>'M'</span><span>:</span> <span>4096</span><span>},</span> <span># values for function arguments not in `x_names` and `y_name`</span>
<span>))</span>
<span>def</span> <span>benchmark</span><span>(</span><span>M</span><span>,</span> <span>N</span><span>,</span> <span>provider</span><span>):</span>
<span>x</span> <span>=</span> <span>torch</span><span>.</span><span>randn</span><span>(</span><span>M</span><span>,</span> <span>N</span><span>,</span> <span>device</span><span>=</span><span>'cuda'</span><span>,</span> <span>dtype</span><span>=</span><span>torch</span><span>.</span><span>float32</span><span>)</span>
<span>stream</span> <span>=</span> <span>torch</span><span>.</span><span>cuda</span><span>.</span><span>Stream</span><span>()</span>
<span>torch</span><span>.</span><span>cuda</span><span>.</span><span>set_stream</span><span>(</span><span>stream</span><span>)</span>
<span>if</span> <span>provider</span> <span>==</span> <span>'torch'</span><span>:</span>
<span>ms</span> <span>=</span> <span>triton</span><span>.</span><span>testing</span><span>.</span><span>do_bench</span><span>(</span><span>lambda</span><span>:</span> <span>torch</span><span>.</span><span>softmax</span><span>(</span><span>x</span><span>,</span> <span>axis</span><span>=-</span><span>1</span><span>))</span>
<span>if</span> <span>provider</span> <span>==</span> <span>'triton'</span><span>:</span>
<span>ms</span> <span>=</span> <span>triton</span><span>.</span><span>testing</span><span>.</span><span>do_bench</span><span>(</span><span>lambda</span><span>:</span> <span>softmax</span><span>(</span><span>x</span><span>))</span>
<span>gbps</span> <span>=</span> <span>lambda</span> <span>ms</span><span>:</span> <span>2</span> <span>*</span> <span>x</span><span>.</span><span>nelement</span><span>()</span> <span>*</span> <span>x</span><span>.</span><span>element_size</span><span>()</span> <span>*</span> <span>1e-9</span> <span>/</span> <span>(</span><span>ms</span> <span>*</span> <span>1e-3</span><span>)</span>
<span>return</span> <span>gbps</span><span>(</span><span>ms</span><span>)</span>
<span>benchmark</span><span>.</span><span>run</span><span>(</span><span>show_plots</span><span>=</span><span>True</span><span>,</span> <span>print_data</span><span>=</span><span>True</span><span>)</span>
<span></span>softmax-performance:
N Triton Torch
0 256.0 478.919310 687.273787
1 384.0 605.411715 819.289040
2 512.0 761.099367 934.683618
3 640.0 785.552905 962.016130
4 768.0 880.073059 1025.759534
5 896.0 927.677054 1058.137819
6 1024.0 983.837789 1108.743692
7 1152.0 1096.790360 614.358556
8 1280.0 1148.233274 668.818744
9 1408.0 1150.227640 720.693012
10 1536.0 1182.473582 782.216974
11 1664.0 1216.574883 814.715998
12 1792.0 1242.628231 854.750376
13 1920.0 1253.575856 907.742024
14 2048.0 1269.852891 953.080248
15 2176.0 1257.273610 974.432016
16 2304.0 1262.677874 1011.595565
17 2432.0 1299.296021 1056.308627
18 2560.0 1306.784949 1082.867302
19 2688.0 1313.819078 1099.897287
20 2816.0 1318.463265 1126.399926
21 2944.0 1322.835757 1166.786437
22 3072.0 1346.370285 1180.412745
23 3200.0 1350.082383 1195.441919
24 3328.0 1360.093837 1225.507456
25 3456.0 1375.795286 1245.904506
26 3584.0 1372.955622 1261.663759
27 3712.0 1386.851514 1269.518524
28 3840.0 1383.941865 1303.207851
29 3968.0 1389.301195 1317.206272
30 4096.0 1397.348688 1324.026193
31 4224.0 1337.787438 1161.983073
32 4352.0 1334.628317 1175.156812
33 4480.0 1357.196330 1181.139507
34 4608.0 1364.957502 1195.702494
35 4736.0 1361.432159 1198.436404
36 4864.0 1378.560609 1219.552557
37 4992.0 1367.111266 1232.723697
38 5120.0 1374.124506 1255.575493
39 5248.0 1378.665107 1261.659380
40 5376.0 1376.411844 1287.514489
41 5504.0 1380.046906 1299.148837
42 5632.0 1382.392228 1315.560426
43 5760.0 1393.669997 1326.327157
44 5888.0 1389.150289 1340.074174
45 6016.0 1398.670392 1350.904213
46 6144.0 1410.218972 1376.087527
47 6272.0 1414.080366 1376.465508
48 6400.0 1416.444662 1385.075582
49 6528.0 1418.413758 1396.029679
50 6656.0 1424.202937 1400.217751
51 6784.0 1409.345707 1415.868223
52 6912.0 1428.837209 1421.806350
53 7040.0 1419.389760 1432.133212
54 7168.0 1424.869740 1433.771252
55 7296.0 1428.331895 1444.078677
56 7424.0 1430.010094 1446.560973
57 7552.0 1423.821714 1456.153560
58 7680.0 1433.745404 1458.530407
59 7808.0 1432.200076 1463.867323
60 7936.0 1433.262612 1465.890268
61 8064.0 1437.370991 1475.045892
62 8192.0 1434.594521 1482.481691
63 8320.0 1386.720429 1399.620234
64 8448.0 1381.399651 1402.663422
65 8576.0 1394.701625 1398.532505
66 8704.0 1384.298625 1400.508376
67 8832.0 1382.690748 1405.417788
68 8960.0 1396.893196 1410.663745
69 9088.0 1407.815867 1416.328473
70 9216.0 1402.560109 1426.002938
71 9344.0 1398.795763 1423.569547
72 9472.0 1398.391728 1434.063187
73 9600.0 1399.009274 1435.793545
74 9728.0 1396.017273 1440.856696
75 9856.0 1414.772213 1440.195824
76 9984.0 1393.640290 1453.226701
77 10112.0 1411.025063 1454.434968
78 10240.0 1416.371231 1466.229997
79 10368.0 1411.954147 1465.497981
80 10496.0 1414.468529 1469.190538
81 10624.0 1408.722590 1467.668473
82 10752.0 1404.295464 1469.379278
83 10880.0 1400.953900 1482.342526
84 11008.0 1420.597508 1474.695685
85 11136.0 1424.100701 1485.490602
86 11264.0 1430.205349 1488.547851
87 11392.0 1411.913312 1489.778907
88 11520.0 1422.768767 1494.569038
89 11648.0 1423.179210 1498.987919
90 11776.0 1431.071404 1500.151596
91 11904.0 1442.538703 1507.563154
92 12032.0 1421.563295 1508.734560
93 12160.0 1419.964136 1509.722295
94 12288.0 1435.906495 1391.634053
95 12416.0 1449.353849 1390.744306
96 12544.0 1441.752742 1392.910081
97 12672.0 1445.543061 1392.769793
In the above plot, we can see that:
-
Triton is 4x faster than the Torch JIT. This confirms our suspicions that the Torch JIT does not do any fusion here.
-
Triton is noticeably faster than
torch.softmax– in addition to being easier to read, understand and maintain. Note however that the PyTorch softmax operation is more general and will work on tensors of any shape.
Total running time of the script: (0 minutes 23.443 seconds)