Berry–Esseen theorem - Wikipedia

In probability theory, the central limit theorem states that, under certain circumstances, the probability distribution of the scaled mean of a random sample converges to a normal distribution as the sample size increases to infinity. Under stronger assumptions, the Berry–Esseen theorem, or Berry–Esseen inequality, gives a more quantitative result, because it also specifies the rate at which this convergence takes place by giving a bound on the maximal error of approximation between the normal distribution and the true distribution of the scaled sample mean. The approximation is measured by the Kolmogorov–Smirnov distance. In the case of independent samples, the convergence rate is n ^−1/2, where n is the sample size, and the constant is estimated in terms of the third absolute normalized moment. It is also possible to give non-uniform bounds which become more strict for more extreme events.

Statements of the theorem vary, as it was independently discovered by two mathematicians, Andrew C. Berry (in 1941) and Carl-Gustav Esseen (1942), who then, along with other authors, refined it repeatedly over subsequent decades.

One version, sacrificing generality somewhat for the sake of clarity, is the following:

There exists a positive constant C such that if X ₁, X ₂,…, are i.i.d. random variables with E (X ₁) = 0, E(X ₁ ²) = σ ² > 0, and E(| X ₁ | ³) = ρ < ∞,¹ and if we define

$Y_n=\frac{X_1+X_2+\cdots +X_n}{n}$

the sample mean, with F _n the cumulative distribution function of

$\frac{Y_n\sqrt{n}}{\sigma },$

and Φ the cumulative distribution function of the standard normal distribution, then for all x and n,

$\left|F_n(x)-\Phi (x)\right|\le \frac{C\rho }{{\sigma }^3\sqrt{n}}.(1)$

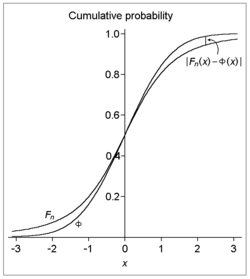
Illustration of the difference in cumulative distribution functions alluded to in the theorem.

That is: given a sequence of independent and identically distributed random variables, each having mean zero and positive variance, if additionally the third absolute moment is finite, then the cumulative distribution functions of the standardized sample mean and the standard normal distribution differ (vertically, on a graph) by no more than the specified amount. Note that the approximation error for all n (and hence the limiting rate of convergence for indefinite n sufficiently large) is bounded by the order of n ^−1/2.

Calculated upper bounds on the constant C have decreased markedly over the years, from the original value of 7.59 by Esseen in 1942.² The estimate C < 0.4748 follows from the inequality

$\underset{x\in \mathbb{R}}{\sup }\left|F_n(x)-\Phi (x)\right|\le \frac{0.33554(\rho +0.415{\sigma }^3)}{{\sigma }^3\sqrt{n}},$

since σ ³ ≤ ρ and 0.33554 · 1.415 < 0.4748. However, if ρ ≥ 1.286 σ ³, then the estimate

$\underset{x\in \mathbb{R}}{\sup }\left|F_n(x)-\Phi (x)\right|\le \frac{0.3328(\rho +0.429{\sigma }^3)}{{\sigma }^3\sqrt{n}},$

is even tighter.³

Esseen (1956) proved that the constant also satisfies the lower bound

$C\ge \frac{\sqrt{10}+3}{6\sqrt{2\pi }}\approx 0.40973\approx \frac{1}{\sqrt{2\pi }}+\mathrm{0.01079.}$

Let X ₁, X ₂,…, be independent random variables with E (X _i) = 0, E(X _i ²) = σ _i ² > 0, and E(| X _i | ³) = ρ _i < ∞. Also, let

$S_n=\frac{X_1+X_2+\cdots +X_n}{\sqrt{{\sigma }_1^2+{\sigma }_2^2+\cdots +{\sigma }_n^2}}$

be the normalized n -th partial sum. Denote F _n the cdf of S _n, and Φ the cdf of the standard normal distribution. For the sake of convenience denote

$\vec{\sigma }=({\sigma }_1,\dots ,{\sigma }_n),\vec{\rho }=({\rho }_1,\dots ,{\rho }_n).$

In 1941, Andrew C. Berry proved that for all n there exists an absolute constant C ₁ such that

$\underset{x\in \mathbb{R}}{\sup }\left|F_n(x)-\Phi (x)\right|\le C_1\cdot {\psi }_1,(2)$

where

${\psi }_1={\psi }_1(\vec{\sigma },\vec{\rho })=(\sum _{i=1}^n{\sigma }_i^2{)}^{-1/2}\cdot \underset{1\le i\le n}{\max }\frac{{\rho }_i}{{\sigma }_i^2}.$

Independently, in 1942, Carl-Gustav Esseen proved that for all n there exists an absolute constant C ₀ such that

$\underset{x\in \mathbb{R}}{\sup }\left|F_n(x)-\Phi (x)\right|\le C_0\cdot {\psi }_0,(3)$

where

${\psi }_0={\psi }_0(\vec{\sigma },\vec{\rho })=(\sum _{i=1}^n{\sigma }_i^2{)}^{-3/2}\cdot \sum _{i=1}^n{\rho }_i.$

It is easy to make sure that ψ ₀ ≤ψ ₁. Due to this circumstance inequality (3) is conventionally called the Berry–Esseen inequality, and the quantity ψ ₀ is called the Lyapunov fraction of the third order. Moreover, in the case where the summands X ₁,…, X _n have identical distributions

${\psi }_0={\psi }_1=\frac{{\rho }_1}{{\sigma }_1^3\sqrt{n}},$

and thus the bounds stated by inequalities (1), (2) and (3) coincide apart from the constant.

Regarding C ₀, obviously, the lower bound established by Esseen (1956) remains valid:

$C_0\ge \frac{\sqrt{10}+3}{6\sqrt{2\pi }}=0.4097\dots .$

The lower bound is exactly reached only for certain Bernoulli distributions (see Esseen (1956) for their explicit expressions).

The upper bounds for C ₀ were subsequently lowered from Esseen’s original estimate 7.59 to 0.5600.⁴

Berry–Esseen theorems exist for the sum of a random number of random variables. The following is Theorem 1 from Korolev (1989), substituting in the constants from Remark 3.⁵ It is only a portion of the results that they established:

Let $\{X_i\}$ be independent, identically distributed random variables with $E(X_i)=\mu$ , $\mathrm{Var}(X_i)={\sigma }^2$ , $E|X_i-\mu {|}^3={\kappa }^3$ . Let $N$ be a non-negative integer-valued random variable, independent from $\{X_i\}$ . Let $S_N=X_1+\cdots +X_N$ , and define

$\Delta =\underset{x}{\sup }\left|P\left(\frac{S_N-E(S_N)}{\sqrt{\mathrm{Var}(S_N)}}\le z\right)-\Phi (z)\right|$

Then

$\Delta \le 3.8696\frac{{\kappa }^3}{\sqrt{E(N)}{\sigma }^3}+1.0395\frac{E|N-E(N)|}{E(N)}+0.2420\frac{{\mu }^2\mathrm{Var}(N)}{{\sigma }^{2}E(N)}$

Multidimensional version

As with the multidimensional central limit theorem, there is a multidimensional version of the Berry–Esseen theorem.^{6 7}

Let $X_1,\dots ,X_n$ be independent ${\mathbb{R}}^d$ -valued random vectors each having mean zero. Write $S_n=\sum _{i=1}^n{X}_i$ and assume ${\Sigma }_n=\mathrm{Cov}[S_n]$ is invertible. Let $Z_n\sim N(0,{\Sigma }_n)$ be a $d$ -dimensional Gaussian with the same mean and covariance matrix as $S_n$ . Then for all convex sets $U\subseteq {\mathbb{R}}^d$ ,

$|\mathrm{Pr}[S_n\in U]-\mathrm{Pr}[Z_n\in U]|\le C{d}^{1/4}{\gamma }_n$ ,

where $C$ is a universal constant and ${\gamma }_n=\sum _{i=1}^{n}E[\Vert {\Sigma }_n^{-1/2}{X}_i{\Vert }_2^3]$ (the third power of the L ² norm).

The dependency on $d^{1/4}$ is conjectured to be optimal, but might not be.⁷

Non-uniform bounds

The bounds given above consider the maximal difference between the cdf’s. They are ‘uniform’ in that they do not depend on $x$ and quantify the uniform convergence $F_n\to \Phi$ . However, because $F_n(x)-\Phi (x)$ goes to zero for large $x$ by general properties of cdf’s, these uniform bounds will be overestimating the difference for such arguments. This is despite the uniform bounds being sharp in general. It is therefore desirable to obtain upper bounds which depend on $x$ and in this way become smaller for large $x$ .

One such result going back to (Esseen 1945) that was since improved multiple times is the following.

As above, let X ₁, X ₂,…, be independent random variables with E (X _i) = 0, E(X _i ²) = σ _i ² > 0, and E(| X _i | ³) = ρ _i < ∞. Also, let ${\sigma }^2=\sum _{i=1}^n{\sigma }_i^2$ and

$S_n=\frac{X_1+X_2+\cdots +X_n}{\sigma }$

be the normalized n -th partial sum. Denote F _n the cdf of S _n, and Φ the cdf of the standard normal distribution. Then

$|F_n(x)-\Phi (x)|\le \frac{C_3}{{\sigma }^3+|x{|}^3}\cdot \sum _{i=1}^n{\rho }_i$ ,

where $C_3$ is a universal constant.

The constant $C_3$ may be taken as 114.667.⁸ Moreover, if the $X_i$ are identically distributed, it can be taken as $C+8(1+\mathrm{e})$ , where $C$ is the constant from the first theorem above, and hence 30.2211 works.⁹

See also

• Chernoff’s inequality
• Edgeworth series
• List of inequalities
• List of mathematical theorems
• Concentration inequality

Notes

References

Bibliography

• Berry, Andrew C. (1941). “The Accuracy of the Gaussian Approximation to the Sum of Independent Variates”. Transactions of the American Mathematical Society. 49 (1): 122– 136. doi:10.1090/S0002-9947-1941-0003498-3. JSTOR 1990053.
• Durrett, Richard (1991). Probability: Theory and Examples. Pacific Grove, CA: Wadsworth & Brooks/Cole. ISBN 0-534-13206-5.
• Esseen, Carl-Gustav (1942). “On the Liapunoff limit of error in the theory of probability”. Arkiv för Matematik, Astronomi och Fysik. A28: 1– 19. ISSN 0365-4133.
• Esseen, Carl-Gustav (1945). “Fourier analysis of distribution functions. A mathematical study of the Laplace-Gaussian law”. Acta Mathematica. 77: 1– 125. doi:10.1007/BF02392223.
• Esseen, Carl-Gustav (1956). “A moment inequality with an application to the central limit theorem”. Skand. Aktuarietidskr. 39: 160– 170.
• Feller, William (1972). An Introduction to Probability Theory and Its Applications, Volume II (2nd ed.). New York: John Wiley & Sons. ISBN 0-471-25709-5.
• Korolev, V. Yu.; Shevtsova, I. G. (2010a). “On the upper bound for the absolute constant in the Berry–Esseen inequality”. Theory of Probability and Its Applications. 54 (4): 638– 658. doi:10.1137/S0040585X97984449.
• Korolev, Victor; Shevtsova, Irina (2010b). “An improvement of the Berry–Esseen inequality with applications to Poisson and mixed Poisson random sums”. Scandinavian Actuarial Journal. 2012 (2): 1– 25. arXiv:0912.2795. doi:10.1080/03461238.2010.485370. S2CID 115164568.
• Manoukian, Edward B. (1986). Modern Concepts and Theorems of Mathematical Statistics. New York: Springer-Verlag. ISBN 0-387-96186-0.
• Serfling, Robert J. (1980). Approximation Theorems of Mathematical Statistics. New York: John Wiley & Sons. ISBN 0-471-02403-1.
• Shevtsova, I. G. (2008). “On the absolute constant in the Berry–Esseen inequality”. The Collection of Papers of Young Scientists of the Faculty of Computational Mathematics and Cybernetics (5): 101– 110.
• Shevtsova, Irina (2007). “Sharpening of the upper bound of the absolute constant in the Berry–Esseen inequality”. Theory of Probability and Its Applications. 51 (3): 549– 553. doi:10.1137/S0040585X97982591.
• Shevtsova, Irina (2010). “An Improvement of Convergence Rate Estimates in the Lyapunov Theorem”. Doklady Mathematics. 82 (3): 862– 864. doi:10.1134/S1064562410060062. S2CID 122973032.
• Shevtsova, Irina (2011). “On the absolute constants in the Berry Esseen type inequalities for identically distributed summands”. arXiv:1111.6554 [math.PR].
• Shiganov, I.S. (1986). “Refinement of the upper bound of a constant in the remainder term of the central limit theorem”. Journal of Soviet Mathematics. 35 (3): 109– 115. doi:10.1007/BF01121471. S2CID 120112396.
• Tyurin, I.S. (2009). “On the accuracy of the Gaussian approximation”. Doklady Mathematics. 80 (3): 840– 843. doi:10.1134/S1064562409060155. S2CID 121383741.
• Tyurin, I.S. (2010). “An improvement of upper estimates of the constants in the Lyapunov theorem”. Russian Mathematical Surveys. 65 (3(393)): 201– 202. doi:10.1070/RM2010v065n03ABEH004688. S2CID 118771013.
• van Beek, P. (1972). “An application of Fourier methods to the problem of sharpening the Berry–Esseen inequality”. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete. 23 (3): 187– 196. doi:10.1007/BF00536558. S2CID 121036017.
• Zolotarev, V. M. (1967). “A sharpening of the inequality of Berry–Esseen”. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete. 8 (4): 332– 342. doi:10.1007/BF00531598. S2CID 122347713.

External links

• Gut, Allan & Holst Lars. Carl-Gustav Esseen, retrieved Mar. 15, 2004.
• “Berry–Esseen inequality”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]

Footnotes

1. Since the random variables are identically distributed, X ₂, X ₃,… all have the same moments as X ₁. ↩

2. Esseen (1942). For improvements see van Beek (1972), Shiganov (1986), Shevtsova (2007), Shevtsova (2008), Tyurin (2009), Korolev & Shevtsova (2010a), Tyurin (2010). The detailed review can be found in the papers Korolev & Shevtsova (2010a) and Korolev & Shevtsova (2010b). ↩

3. Shevtsova (2011). ↩

4. Esseen (1942); Zolotarev (1967); van Beek (1972); Shiganov (1986); Tyurin (2009); Tyurin (2010); Shevtsova (2010). ↩

5. Korolev, V. Yu (1989). “On the Accuracy of Normal Approximation for the Distributions of Sums of a Random Number of Independent Random Variables”. Theory of Probability & Its Applications. 33 (3): 540– 544. doi:10.1137/1133079. ↩

6. Bentkus, Vidmantas. “A Lyapunov-type bound in R ^d.” Theory of Probability & Its Applications 49.2 (2005): 311–323. ↩

7. Raič, Martin (2019). “A multivariate Berry—Esseen theorem with explicit constants”. Bernoulli. 25 (4A): 2824– 2853. arXiv:1802.06475. doi:10.3150/18-BEJ1072. ISSN 1350-7265. S2CID 119607520. ↩ ↩²

8. Paditz, Ludwig (1997). Über die Annäherung der Verteilungsfunktionen von Summen unabhängiger Zufallsgrößen gegen unbegrenzt teilbare Verteilungsfunktionen unter besonderer Beachtung der Verteilungsfunktion der standardisierten Normalverteilung [On the approximation of cumulative distribution functions of sums of independent random variables by infinitely divisible cumulative distribution functions with special attention to the cumulative distribution function of the standard normal distribution] (in German). Dresden. p. 6.{{[cite book](https://en.wikipedia.org/wiki/Template:Cite_book "Template:Cite book")}}: CS1 maint: location missing publisher (link) ↩

9. Michel, R. (1981). “On the constant in the nonuniform version of the Berry-Esséen theorem”. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete. 55: 109– 117. ↩